题目内容
9．化简求值：（$\frac{a+1}{{a}^{2}-a}+\frac{4}{1-{a}^{2}}$）÷$\frac{{a}^{2}+2a-3}{{a}^{2}+3a}$，其中a=2tan60°-1．分析 原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分得到最简结果，求出a的值代入计算即可求出值．
解答 解：原式=$\frac{（a+1）^{2}-4a}{a（a+1）（a-1）}$•$\frac{a（a+3）}{（a-1）（a+3）}$=$\frac{（a-1）^{2}}{a（a+1）（a-1）}$•$\frac{a（a+3）}{（a-1）（a+3）}$=$\frac{1}{a+1}$，
当a=2tan60°-1=2$\sqrt{3}$-1时，原式=$\frac{\sqrt{3}}{6}$．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
19．
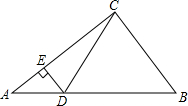如图，在Rt△ABC中，∠ACB=90°，tanB=$\frac{4}{3}$，点D，E分别在边AB，AC上，DE⊥AC，DE=6，DB=20，则tan∠BCD的值是$\frac{8}{3}$．
如图，在Rt△ABC中，∠ACB=90°，tanB=$\frac{4}{3}$，点D，E分别在边AB，AC上，DE⊥AC，DE=6，DB=20，则tan∠BCD的值是$\frac{8}{3}$．
20．
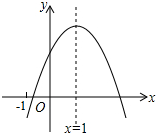二次函数y=ax2+bx+c（a≠0）的图象如图所示，其对称轴为x=1，下列结论中错误的是（ ）
二次函数y=ax2+bx+c（a≠0）的图象如图所示，其对称轴为x=1，下列结论中错误的是（ ）| A． | abc＜0 | B． | 2a+b=0 | C． | b2-4ac＞0 | D． | a-b+c＞0 |
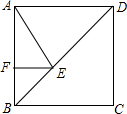如图，正方形ABCD的边长为4+2$\sqrt{2}$，点E在对角线BD上，且∠BAE=22.5°，EF⊥AB，垂足为点F，则EF的长是2．
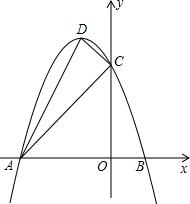如图，二次函数y=ax2+bx+c（a＜0）图象的顶点为D，与x轴的两个交点分别为A、B（A在B左侧），与y轴交于点C（0，3），且OA=3OB，∠ACD=90°