题目内容
已知Rt△ABC和Rt△EBC,°。以边AC上的点O为圆心、OA为半径的⊙O与EC相切,D为切点,AD//BC。
(1)用尺规确定并标出圆心O;(不写做法和证明,保留作图痕迹)
(2)求证:
(3)若AD=1,,求BC的长。(8分)
(1)略
(2)略
(3)2
解析:解:
(1)(提示:O即为AD中垂线与AC的交点或过D点作EC的垂线与AC的交点等).
能见作图痕迹,作图基本准确即可,漏标O可不扣分 2分
(2)证明:连结OD.∵AD∥BC , ∠B=90°,∴∠EAD=90°.
∴∠E+∠EDA=90°,即∠E=90°-∠EDA.
又圆O与EC相切于D点,∴OD⊥EC.
∴∠EDA+∠ODA=90°,即∠ODA=90°-∠EDA.
∴∠E=∠ODA 3分
(说明:任得出一个角相等都评1分)
又OD=OA,∴∠DAC=∠ODA,∴∠DAC=∠E. 4分
∵AD∥BC,∴∠DAC=∠ACB,∴∠E=∠ACB. 5分
(3)Rt△DEA中,tan∠E=,又tan∠E=tan∠DAC=
,
∵AD=1∴EA=. 6分
Rt△ABC中,tan∠ACB=,
又∠DAC=∠ACB,∴tan∠ACB=tan∠DAC.
∴=
,∴可设
.
∵AD∥BC,∴Rt△EAD∽Rt△EBC. 7分
∴,即
.
∴,∴
. 8分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
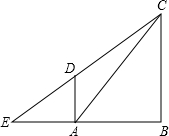 相切,D为切点,AD∥BC.
相切,D为切点,AD∥BC.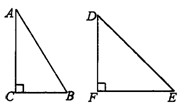 14、如图,已知Rt△ABC和Rt△DEF不相似,其中∠C,∠F为直角,∠A<∠D,能否分别将两个三角形分割成两个三角形,使△ABC所分的两个三角形与△DEF所分的两个三角形分别相似?如果能够,请设计一个分割方案;如果不能,请说明理由.
14、如图,已知Rt△ABC和Rt△DEF不相似,其中∠C,∠F为直角,∠A<∠D,能否分别将两个三角形分割成两个三角形,使△ABC所分的两个三角形与△DEF所分的两个三角形分别相似?如果能够,请设计一个分割方案;如果不能,请说明理由.
 如图,已知Rt△ABC和三角形外一点P,按要求完成图形:
如图,已知Rt△ABC和三角形外一点P,按要求完成图形: