题目内容
已知Rt△ABC和Rt△ADC有公共斜边AC,M、N分别是AC、BD的中点,且M、N不重合,请你画出图形后回答,线段MN与BD是否垂直?并请说明理由.若∠BAC=30°,∠CAD=45°,AC=8cm,求MN的长.分析:根据题意画出图形后可知本题有两种情况,即B、D在线段AC的同侧和B、D在线段AC的异侧.
解答:解:如图一:连接BM、MD,延长DM,过B作DM延长线的垂线段BE,
则可知在Rt△BEM中∠EMB=30°,
∵AC=8,∴BM=4,
∴BE=2,EM=2
,MD=4,
从而可知BD=
=4
,
∴MN=
=(
-
)cm,
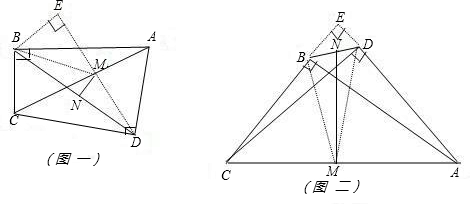
如图二:连接BM、MD,延长AD,过B作垂线段BE,在Rt△BED中,可知∠EDB=60°,
令ED=x,则BE=
x,AD=4
,AB=4
,
∴可得:(4
)2=(
x)2+(x+4
)2,
解得x=
-
,
∴MN=
=(
+
)cm.
则可知在Rt△BEM中∠EMB=30°,
∵AC=8,∴BM=4,
∴BE=2,EM=2
| 3 |
从而可知BD=
22+(2
|
2+
|
∴MN=
42-(2
|
| 6 |
| 2 |

如图二:连接BM、MD,延长AD,过B作垂线段BE,在Rt△BED中,可知∠EDB=60°,
令ED=x,则BE=
| 3 |
| 2 |
| 3 |
∴可得:(4
| 3 |
| 3 |
| 2 |
解得x=
| 6 |
| 2 |
∴MN=
| 42-x2 |
| 6 |
| 2 |
点评:本题考查了勾股定理的应用及直角三角形的相关知识,解决此题很容易漏掉另外一种情况.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
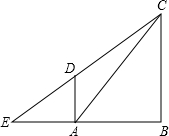 相切,D为切点,AD∥BC.
相切,D为切点,AD∥BC.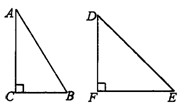 14、如图,已知Rt△ABC和Rt△DEF不相似,其中∠C,∠F为直角,∠A<∠D,能否分别将两个三角形分割成两个三角形,使△ABC所分的两个三角形与△DEF所分的两个三角形分别相似?如果能够,请设计一个分割方案;如果不能,请说明理由.
14、如图,已知Rt△ABC和Rt△DEF不相似,其中∠C,∠F为直角,∠A<∠D,能否分别将两个三角形分割成两个三角形,使△ABC所分的两个三角形与△DEF所分的两个三角形分别相似?如果能够,请设计一个分割方案;如果不能,请说明理由.
 如图,已知Rt△ABC和三角形外一点P,按要求完成图形:
如图,已知Rt△ABC和三角形外一点P,按要求完成图形: