题目内容
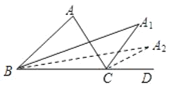
【题目】如图,在△ABC中,∠A=β度,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线交于点A2,得∠A2,…∠A2017BC与∠A2017CD的平分线交于点A2018,得∠A2018.则∠A2018=_____度.
【答案】![]()
【解析】
设∠ABC=2α,所以∠ACD=2α+β,由角平分线的性质可知∠A1CD=![]() ∠ACD=
∠ACD=![]() +α,∠A1BC=
+α,∠A1BC=![]() ∠ABC=α,由三角形的外角性质可知∠A1=
∠ABC=α,由三角形的外角性质可知∠A1=![]() ,同理可求出∠A2=
,同理可求出∠A2=![]() ,∠A3=
,∠A3=![]() ,根据规律即可求出∠A2018=
,根据规律即可求出∠A2018=![]() .
.
设∠ABC=2α,
∴∠ACD=2α+β,
∵∠ABC与∠ACD的平分线交于点A1
∴∠A1CD=![]() ∠ACD=
∠ACD=![]() +α,∠A1BC=
+α,∠A1BC=![]() ∠ABC=α,
∠ABC=α,
∵∠A1CD=∠A1BC+∠A1,
∴∠A1=![]()
同理可得:∠A2=![]() ,∠A3=
,∠A3=![]() ,
,
∴∠A2018=![]()
故答案为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目