题目内容
14.某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:| 单价(元/件) | 30 | 34 | 38 | 40 | 42 |
| 销量(件) | 40 | 32 | 24 | 20 | 16 |
(2)通过对上面表格中的数据进行分析,发现销量y(件)与单价x(元/件)之间存在一次函数关系,求y关于x的函数关系式(不需要写出函数自变量的取值范围);
(3)预计在今后的销售中,销量与单价仍然存在(2)中的关系,且该产品的成本是20元/件.为使工厂获得最大利润,该产品的单价应定为多少?
分析 (1)根据题中表格中的数据列出算式,计算即可得到结果;
(2)设y=kx+b,从表格中找出两对值代入求出k与b的值,即可确定出解析式;
(3)设定价为x元时,工厂获得的利润为W,列出W与x的二次函数解析式,利用二次函数性质求出W最大时x的值即可.
解答 解:(1)根据题意得:$\frac{30×40+34×32+38×24+40×20+42×16}{5}$=934.4(元);
(2)根据题意设y=kx+b,
把(30,40)与(40,20)代入得:$\left\{\begin{array}{l}{30k+b=40}\\{40k+b=20}\end{array}\right.$,
解得:k=-2,b=100,
则y=-2x+100;
(3)设定价为x元时,工厂获得的利润为W,
根据题意得:W=(x-20)y=(x-20)(-2x+100)=-2x2+140x-2000=-2(x-35)2+450,
∵当x=35时,W最大值为450,
则为使工厂获得最大利润,该产品的单价应定为35元.
点评 此题考查了二次函数的应用,待定系数法确定一次函数解析式,以及二次函数的性质,熟练掌握二次函数性质是解本题的关键.

练习册系列答案
相关题目
4.a2的算术平方根一定是( )
| A. | a | B. | |a| | C. | $\sqrt{a}$ | D. | -a |
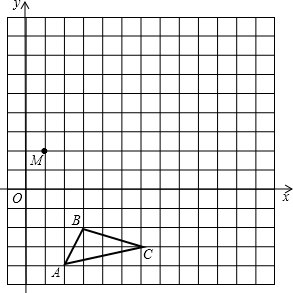 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3). 作△ABC关于点O成中心对称的△A′B′C′.
作△ABC关于点O成中心对称的△A′B′C′.