Question

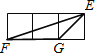
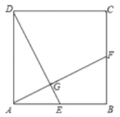
【题目】如图，矩形纸片ABCD，BC=10，AB=8，E是边CD上一点，连接AE、折叠该纸片，使点A落在AE上的G点，并使折痕经过点B，得到折痕BF，点F在AD上，若DE=5，则GE的长为____．

Answer 1

【答案】．

【解析】

由勾股定理求出AE的长，证明△ABH∽△EAD，得出求出AH的长，得出AG的长，即可得出答案．

∵四边形ABCD为矩形，

∴AB=CD=8，AD=BC=10，∠BAD=∠D=90°，

∴AE5，

由折叠及轴对称的性质可知，△ABF≌△GBF，BF垂直平分AG，

∴BF⊥AE，AH=GH，

∴∠BAH+∠ABH=90°，

又∵∠FAH+∠BAH=90°，

∴∠ABH=∠FAH，

∴△ABH∽△EAD，

∴，即，

解得：AH，

∴AG=2AH，

∴GE=AE﹣AG=5．

故答案为：．