题目内容
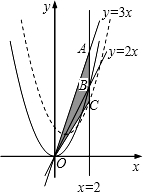如图，直线y=3x和y=2x分别与直线x=2相交于点A、B，将抛物线y=x2沿线段OB移动，使其顶点始终在线段OB上，抛物线与直线x=2相交于点C，设△AOC的面积为S，求S的取值范围．考点：二次函数图象与几何变换
专题：
分析：要求△AOC的面积，先用a表示出AC的长度，AC边上的高等于2，所以三角形AOC的面积=
×AC×2，然后整理出面积和a的函数关系式，求出S的范围．
| 1 |
| 2 |
解答：解：设抛物线平移到顶点P（a，2a）处，其解析式为y=（x-a）2+2a与直线x=2的交点C（2，（2-a）2+2a），A（2，6）
AC=6-（2-a）2-2a，
S=2[6-（2-a）2-2a]/2
=6-4+4a-a2-2a
=-a2+2a+2
当0≤a≤2时，有最大值：a=1时，S最大=3；当a=0或2时S最小=2．
故S的取值范围是2≤S≤3．
AC=6-（2-a）2-2a，
S=2[6-（2-a）2-2a]/2
=6-4+4a-a2-2a
=-a2+2a+2
当0≤a≤2时，有最大值：a=1时，S最大=3；当a=0或2时S最小=2．
故S的取值范围是2≤S≤3．
点评：主要考查二次函数的性质，根据二次函数的性质求最值．
练习册系列答案
相关题目
下列四个数中的负数是（ ）
| A、-22 | ||
B、
| ||
| C、（-2）2 | ||
| D、|-2| |
如图，四边形ABCD为菱形，已知A（0，4），B（-3，0）．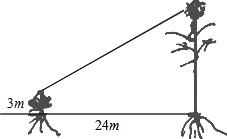
有一只喜鹊在一棵3m高的小树上觅食，它的巢筑在距离该树24m的一棵大树上，大树高14m，且巢离树顶部1m．当它听到巢中幼鸟的叫声，立即赶过去，如果它飞行的速度为5.2m/s，那它至少需要多少时间才能赶回巢中？
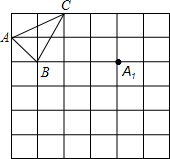作图题：如图是6×6的网格，已知格点△ABC和格点A1．
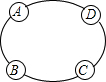如图是某汽车维修公司的维修点在环形公路上的分布图．公司在年初分配给A，B，C，D四个维修点某种配件各50件．在使用前发现需将A，B，C，D四个维修点的这批配件分别调整为40，45，54，61件，但调整只能在相邻维修点之间进行，那么要完成上述调整，最少的调动件次为多少？说明理由．（注：n件配件从一个维修点调整到相邻维修点的调动件次为n）
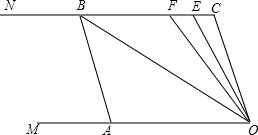如图，已知两条射线OM∥CN，动线段AB的两个端点A、B分别在射线OM、CN上，且∠C=∠OAB=108°，F在线段CB上，OB平分∠AOF，OE平分∠COF．