题目内容
19.当m=-$\frac{1}{3}$时,分式方程$\frac{mx}{m+1}$-$\frac{2}{x+2}$=1的解与分式方程$\frac{x+4}{x}$=3的解互为相反数.分析 先解分式方程$\frac{x+4}{x}$=3,再把x的值代入分式方程$\frac{mx}{m+1}$-$\frac{2}{x+2}$=1,即可得出m的值.
解答 解:解分式方程$\frac{x+4}{x}$=3,得x=2,
经检验,x=2是原方程的解;
∵分式方程$\frac{mx}{m+1}$-$\frac{2}{x+2}$=1的解与分式方程$\frac{x+4}{x}$=3的解互为相反数,
∴分式方程$\frac{mx}{m+1}$-$\frac{2}{x+2}$=1的解为x=-2,
把x=-2代入分式方程$\frac{mx}{m+1}$-$\frac{2}{x+2}$=1得,$\frac{-2m}{m+1}$=1,
解得m=-$\frac{1}{3}$,
经检验m=-$\frac{1}{3}$是方程-$\frac{2m}{m+1}$=1的解,
故答案为-$\frac{1}{3}$.
点评 本题考查了解分式方程,解分式方程一定要验根.

练习册系列答案
相关题目
9.若正六边形的半径长为4,则它的边长等于( )
| A. | 4 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
7.点P(-|a|-1,b2+2)一定在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11. 如图,在?ABCD中,若M为BC边的中点,AM与BD交于点N,那么S△BMN:S?ABCD=( )
如图,在?ABCD中,若M为BC边的中点,AM与BD交于点N,那么S△BMN:S?ABCD=( )
 如图,在?ABCD中,若M为BC边的中点,AM与BD交于点N,那么S△BMN:S?ABCD=( )
如图,在?ABCD中,若M为BC边的中点,AM与BD交于点N,那么S△BMN:S?ABCD=( )| A. | 1:12 | B. | 1:9 | C. | 1:8 | D. | 1:6 |
9.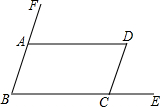 如图,在平行四边形ABCD中,点E、F分别在BC、BA的延长线上,∠DCE=65°,则∠FAD的大小是( )
如图,在平行四边形ABCD中,点E、F分别在BC、BA的延长线上,∠DCE=65°,则∠FAD的大小是( )
 如图,在平行四边形ABCD中,点E、F分别在BC、BA的延长线上,∠DCE=65°,则∠FAD的大小是( )
如图,在平行四边形ABCD中,点E、F分别在BC、BA的延长线上,∠DCE=65°,则∠FAD的大小是( )| A. | 115° | B. | 25° | C. | 65° | D. | 35° |