题目内容
9. 如图,△ABC中,BC=AC,∠ACB=90°,将△ABC绕着点C顺时针旋转α°(0≤α≤90°),得到△EFC,EF与AB、AC相交于点D、H,FC与AB相交于点G、AC相交于点D、H,FC与AB相较于点G.
如图,△ABC中,BC=AC,∠ACB=90°,将△ABC绕着点C顺时针旋转α°(0≤α≤90°),得到△EFC,EF与AB、AC相交于点D、H,FC与AB相交于点G、AC相交于点D、H,FC与AB相较于点G.(1)求证:△GBC≌△HEC;
(2)在旋转过程中,四边形BCED可以是某种特殊的平行四边形?并说明理由.
分析 (1)先判断△ABC为等腰直角三角形得到∠A=∠B=45°,再根据旋转的性质得∠BCF=∠ACE=α,∠E=∠A=45°,CA=CE=CB,于是可根据“ASA”判断△GBC≌△HEC;
(2)当α=45°时,如图,根据旋转的性质得∠BCF=∠ACE=45°,则可计算出∠BCE=∠BCA+∠ACE=135°,所以∠B+∠BCE=180°,∠E+∠BCE=180°,所以BD∥CE,BC∥DE,于是可判断四边形BCED为平行四边形,加上CB=CE,则可判断四边形BCED为菱形.
解答 (1)证明:∵BC=AC,∠ACB=90°,
∴△ABC为等腰直角三角形,
∴∠A=∠B=45°,
∵△ABC绕着点C顺时针旋转α°(0≤α≤90°),得到△EFC,
∴∠BCF=∠ACE=α,∠E=∠A=45°,CA=CE=CB,
在△GBC和△HEC中
$\left\{\begin{array}{l}{∠B=∠E}\\{CB=CE}\\{∠BCG=∠ECH}\end{array}\right.$,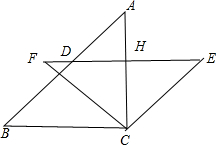
∴△GBC≌△HEC;
(2)解:当α=45°时,四边形BCED为菱形.理由如下:
如图,∵∠BCF=∠ACE=45°,
∴∠BCE=∠BCA+∠ACE=90°+45°=135°,
而∠E=∠B=45°,
∴∠B+∠BCE=180°,∠E+∠BCE=180°,
∴BD∥CE,BC∥DE,
∴四边形BCED为平行四边形,
∵CB=CE,
∴四边形BCED为菱形.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是掌握菱形的判定方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14. 已知二次函数y=x2+bx+c的图象如图所示,若y>0,则x的取值范围是( )
已知二次函数y=x2+bx+c的图象如图所示,若y>0,则x的取值范围是( )
 已知二次函数y=x2+bx+c的图象如图所示,若y>0,则x的取值范围是( )
已知二次函数y=x2+bx+c的图象如图所示,若y>0,则x的取值范围是( )| A. | -1<x<3 | B. | -1<x<4 | C. | x<-1或x>3 | D. | x<-1或x>4 |
11.下列说法正确的是( )
| A. | 90°的角叫余角,180°的角叫补角 | |
| B. | 如果∠1+∠2+∠3=180°,那么∠1、∠2与∠3互补 | |
| C. | 如果两个角相等,那么它们的补角相等 | |
| D. | 如果∠α>∠β,那么∠α的补角比∠β的补角大 |
 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),在建立的平面直角坐标系中,△ABC绕旋转中心P逆时针旋转90°后得到△A1B1C1.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),在建立的平面直角坐标系中,△ABC绕旋转中心P逆时针旋转90°后得到△A1B1C1. 如图,△ABC中,AD是高,E、F分别是AB、AC的中点.若AB=10,AC=8,则四边形AEDF的周长为18.
如图,△ABC中,AD是高,E、F分别是AB、AC的中点.若AB=10,AC=8,则四边形AEDF的周长为18.