题目内容
因式分解：4a2-4ab+b2-6a+3b-4．
考点：因式分解-分组分解法,因式分解-十字相乘法等
专题：
分析：根据分组，可得完全平方公式，根据十字相乘法，可得答案．
解答：解：原式=（4a2-4ab+b2）+（-6a+3b）-4
=（2a-b）2-3（2a-b）-4
=[（2a-b）-4][（2a-b）+1]
=（2a-b-4）（2a-b+1）．
=（2a-b）2-3（2a-b）-4
=[（2a-b）-4][（2a-b）+1]
=（2a-b-4）（2a-b+1）．
点评：本题考查了因式分解，先分组分解，再用十字相乘法分解．
练习册系列答案
相关题目
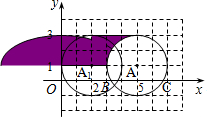如图，在平面直角坐标系中，以A（5，1）为圆心，2个单位长度为半径的⊙A交x轴于点B、C．解答下列问题：
如图所示，在△ABC中，∠ABC=∠C=∠BDC，∠A=∠ABD，求∠A的度数．
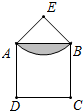如图所示，△EBA是等边三角形，□ABCD边长为6，E是过A、B两点圆弧的圆心，求阴影部分面积．
如图，点A，B，C，D，E均在⊙O上，则∠A+∠B+∠C+∠D+∠E=