题目内容
如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.
(1)若∠B=70°,则∠NMA的度数是__________;
(2)探究∠B与∠NMA的关系,并说明理由;
(3)连接MB,若AB=8cm,△MBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在点P,使PB+CP的值最小?若存在,标出点P的位置并求PB+CP的最小值;若不存在,说明理由.
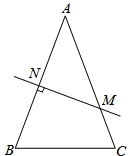
【考点】轴对称-最短路线问题;线段垂直平分线的性质;等腰三角形的性质.
【分析】(1)根据等腰三角的性质,三角形的内角和定理,可得∠A的度数,根据直角三角形两锐角的关系,可得答案;
(2)根据等腰三角的性质,三角形的内角和定理,可得∠A的度数,根据直角三角形两锐角的关系,可得答案;
(3)根据垂直平分线的性质,可得AM与MB的关系,再根据三角形的周长,可得答案;根据两点之间线段最短,可得P点与M点的关系,可得PB+PC与AC的关系.
【解答】解:(1)若∠B=70°,则∠NMA的度数是 50°,
故答案为:50°;
(2)猜想的结论为:∠NMA=2∠B﹣90°.
理由:∵AB=AC,
∴∠B=∠C,
∴∠A=180°﹣2∠B,
又∵MN垂直平分AB,
∴∠NMA=90°﹣∠A=90°﹣(180°﹣2∠B)=2∠B﹣90°.
(3)如图:
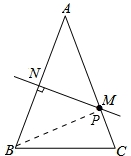
①∵MN垂直平分AB.
∴MB=MA,
又∵△MBC的周长是14cm,
∴AC+BC=14cm,
∴BC=6cm.
②当点P与点M重合时,PB+CP的值最小,最小值是8cm.
【点评】本题考查了轴对称,线段垂直平分线上的点到线段两端点的距离相等得出PB=PA.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目


 )3÷(
)3÷( )2
)2 2,其中a=
2,其中a= ,b=
,b= .
.
 中的x和y都扩大3倍,那么分式的值( )
中的x和y都扩大3倍,那么分式的值( )



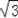
 sin60°﹣2cos45°.
sin60°﹣2cos45°.