题目内容
7.为了抓住世博会商机,某商店决定购进A、B两种世博会纪念品,若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定拿出4000元全部用来购进这两种纪念品,考虑市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B钟纪念品数量的8倍,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少?
分析 (1)设我校购进一件A种纪念品需要a元,购进一件B种纪念品需要b元,根据条件建立二元一次方程组求出其解即可;
(2)设我校购进A种纪念品x个,购进B种纪念品y个,根据条件的数量关系建立不等式组求出其解即可;
(3)设总利润为W元,根据总利润=两种商品的利润之和建立解析式,由解析式的性质就可以求出结论.
解答 解:(1)设我校购进一件A种纪念品需要a元,购进一件B种纪念品需要b元,由题意,得
$\left\{\begin{array}{l}{10a+5b=1000}\\{5a+3b=550}\end{array}\right.$,
∴解方程组得:$\left\{\begin{array}{l}{a=50}\\{b=100}\end{array}\right.$
答:购进一件A种纪念品需要50元,购进一件B种纪念品需要100元.
(2)设我校购进A种纪念品x个,购进B种纪念品y个,由题意,得
则$\left\{\begin{array}{l}{50x+100y=4000}\\{6y≤x≤8y}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=80-2y}\\{6y≤x≤8y}\end{array}\right.$,
解得:8≤y≤10
∵y为正整数
∴y=8,9,10
答:共有3种进货方案;
(3)设总利润为W元,由题意,得
W=20x+30y=20(80-2 y)+30y,
=-10y+4000(20≤y≤25)
∵-10<0,
∴W随y的增大而减小,
∴当y=8时,W有最大值
W最大=-10×8+4000=3920(元)
答:当购进A种纪念品64件,B种纪念品8件时,可获最大利润,最大利润是3920元.
点评 本题考查了待定系数法求一次函数的解析式的运用,列一元一次不等式解实际问题的运用,一次函数的性质的运用,解答时求出一次函数的解析式是关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | -(-2) | B. | -|-2| | C. | -22 | D. | (-2)2 |
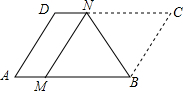 如图,将平行四边形纸片ABCD折叠,使顶点C恰好落在AB边上的点M处,折痕为BN,则关于结论:①MN∥AD;②MNCB是菱形.说法正确的是( )
如图,将平行四边形纸片ABCD折叠,使顶点C恰好落在AB边上的点M处,折痕为BN,则关于结论:①MN∥AD;②MNCB是菱形.说法正确的是( )| A. | ①②都错 | B. | ①对②错 | C. | ①错②对 | D. | ①②都对 |
 将“创建文明城市”六个字分别写在一个正方体的六个面上,这个正方体的平面展开图如图所示,那么在这个正方体中,和“创”相对的字是明.
将“创建文明城市”六个字分别写在一个正方体的六个面上,这个正方体的平面展开图如图所示,那么在这个正方体中,和“创”相对的字是明. 如图,点B、D、C、F在一条直线上,BC=FD,AB=EF,且AB∥EF.求证:AC∥ED.
如图,点B、D、C、F在一条直线上,BC=FD,AB=EF,且AB∥EF.求证:AC∥ED. 如图,矩形ABCD中,AC、BD交于点O,AE⊥BD于E,DE=EO,0F⊥AB于F,0F=3cm,则BD=12cm.
如图,矩形ABCD中,AC、BD交于点O,AE⊥BD于E,DE=EO,0F⊥AB于F,0F=3cm,则BD=12cm.