题目内容
某大型超市国庆期间举行促销活动.假定一次购物不超过100元的不给优惠;超过100元而不超过300元时,按该次购物金额9折优惠;超过300元的其中300元仍按9折优惠,超过300元部分按8折优惠.小美两次购物分别用了94.5元和282.8元,现小丽决定一次购买小美分两次购买的同样的物品,应付款多少元?
考点:一元一次方程的应用
专题:
分析:由100×0.9=90<94.5<100,300×0.9=270<282.8,设小美第二次购物的原价为x元,根据购物付282.8元可得方程,求得解.解大于300元时要分两种情况情况考虑小丽应该付的钱数:①小美第一次购物没有优惠,第二次购物原价超过300元;②小美第一次购物原价超过100元,第二次购物原价超过300元.分别列出代数式求解.
解答:解:因为100×0.9=90<94.5<100,300×0.9=270<282.8,
设小美第二次购物的原价为x元,
则(x-300)×0.8+300×0.9=282.8解得,x=316
所以有两种情况:
情况1:小美第一次购物没有优惠,第二次购物原价超过300元
则小丽应付(316+94.5-300)×0.8+300×0.9=358.4(元)
情况2:小美第一次购物原价超过100元,第二次购物原价超过300元;
则第一次购物原价为:94.5÷0.9=105(元)
所以小丽应付(316+105-300)×0.8+300×0.9=366.8(元).
答:小丽应该付款358.4元或366.8元.
设小美第二次购物的原价为x元,
则(x-300)×0.8+300×0.9=282.8解得,x=316
所以有两种情况:
情况1:小美第一次购物没有优惠,第二次购物原价超过300元
则小丽应付(316+94.5-300)×0.8+300×0.9=358.4(元)
情况2:小美第一次购物原价超过100元,第二次购物原价超过300元;
则第一次购物原价为:94.5÷0.9=105(元)
所以小丽应付(316+105-300)×0.8+300×0.9=366.8(元).
答:小丽应该付款358.4元或366.8元.
点评:本题考查了一元一次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,注意分情况讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
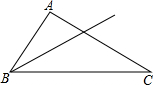 如图,在△ABC中,∠A=105°,直线BD交AC于D,把三角形沿着直线BD翻折,点A恰好落在边CB上,如果△CBD是等腰三角形,那么∠C等于( )
如图,在△ABC中,∠A=105°,直线BD交AC于D,把三角形沿着直线BD翻折,点A恰好落在边CB上,如果△CBD是等腰三角形,那么∠C等于( )| A、15° | B、25° |
| C、30° | D、40° |
 如图,△ABC中,AB=AC=CD,BD=AD,求△ABC中各角的度数.
如图,△ABC中,AB=AC=CD,BD=AD,求△ABC中各角的度数.