题目内容
17.一质点P从距原点1个单位的M点处向原点方向跳动,第一次跳动到OM的中点M3处,第二次从M3跳到OM3的中点M2处,第三次从点M2跳到OM2的中点M1处,如此不断跳动下去,则第n次跳动后,该质点到原点O的距离为$\frac{1}{{2}^{n}}$.
分析 根据每次跳动都是原来的$\frac{1}{2}$,可得答案.
解答 解:第一次跳动到OM的中点M3处,得OM3=$\frac{1}{2}$,
第二次从M3跳到OM3的中点M2处,得OM2=$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{{2}^{2}}$,
第三次从点M2跳到OM2的中点M1处,得OM1=$\frac{1}{2}$×$\frac{1}{{2}^{2}}$=$\frac{1}{{2}^{3}}$,
则第n次跳动后,该质点到原点O的距离为$\frac{1}{{2}^{n}}$,
故答案为:$\frac{1}{{2}^{n}}$.
点评 本题考查了规律型,发现规律:每次跳动都是原来的$\frac{1}{2}$是解题关键.

练习册系列答案
相关题目
 如图,AC⊥CB,DB⊥CB,AB=DC,AB与CD相交于点E.
如图,AC⊥CB,DB⊥CB,AB=DC,AB与CD相交于点E.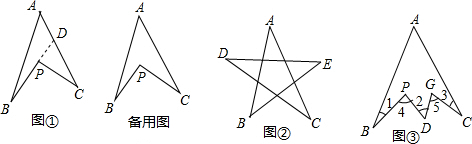
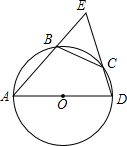 如图,四边形ABCD内接于⊙O,AD是⊙O的直径,C是$\widehat{BD}$的中点,AB与DC的延长线交⊙O外一点E.试判定△EAD和△EBC的形状,并证明你的结论.
如图,四边形ABCD内接于⊙O,AD是⊙O的直径,C是$\widehat{BD}$的中点,AB与DC的延长线交⊙O外一点E.试判定△EAD和△EBC的形状,并证明你的结论.