题目内容
 如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A、C分别在x、y轴上,反比例函数y=
如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A、C分别在x、y轴上,反比例函数y=| k |
| x |
①△OCN≌△OAM;
②ON=MN;
③四边形DAMN与△MON面积相等;
④若∠MON=45°,MN=2,则点C的坐标为(0,
| 2 |
其中正确结论的有
考点:反比例函数综合题
专题:综合题
分析:设正方形OABC的边长为a,表示出A,B,C,M,N的坐标,利用SAS得到三角形OCN与三角形OAM全等,结论①正确;利用勾股定理表示出ON与MN,即可对于结论②做出判断;利用反比例函数的性质得到三角形OCN与三角形OAM全等,根据三角形MON面积=三角形OND面积+四边形ADNM面积-三角形OAM面积,等量代换得到四边形DAMN与△MON面积相等,结论③正确;过O作OH垂直于MN,如图所示,利用ASA得到三角形OCN与三角形OHN全等,利用全等三角形对应边相等得到CN=HN=1,求出a的值,确定出C坐标,即可对于结论④做出判断.
解答:解:设正方形OABC的边长为a,
得到A(a,0),B(a,a),C(0,a),M(a,
),N(
,a),
在△OCN和△OAM中,
,
∴△OCN≌△OAM(SAS),结论①正确;
根据勾股定理,ON=
=
=
,MN=
=
|a2-k|,
∴ON和MN不一定相等,结论②错误;
∵S△ODN=S△OAM,
∴S△MON=S△ODN+S四边形DAMN-S△OAM=S四边形DAMN,结论③正确;
过点O作OH⊥MN于点H,如图所示,
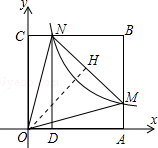
∵△OCN≌△OAM,
∴ON=OM,∠CON=∠AOM,
∵∠MON=45°,MN=2,
∴NH=HM=1,∠CON=∠NOH=∠HOM=∠AOM=22.5°,
∴△OCN≌△OHN(ASA),
∴CN=HN=1,
∴
=1,即k=a,
由MN=
|a2-k|得,2=
|a2-a|,
整理得:a2-2a-1=0,
解得:a=
=1±
(舍去负值),
∴点C的坐标为(0,
+1),结论④正确,
则结论正确的为①③④,
故答案为:①③④
得到A(a,0),B(a,a),C(0,a),M(a,
| k |
| a |
| k |
| a |
在△OCN和△OAM中,
|
∴△OCN≌△OAM(SAS),结论①正确;
根据勾股定理,ON=
| OC2+CN2 |
a2+(
|
| 1 |
| a |
| a4+k2 |
2(a-
|
| ||
| a |
∴ON和MN不一定相等,结论②错误;
∵S△ODN=S△OAM,
∴S△MON=S△ODN+S四边形DAMN-S△OAM=S四边形DAMN,结论③正确;
过点O作OH⊥MN于点H,如图所示,

∵△OCN≌△OAM,
∴ON=OM,∠CON=∠AOM,
∵∠MON=45°,MN=2,
∴NH=HM=1,∠CON=∠NOH=∠HOM=∠AOM=22.5°,
∴△OCN≌△OHN(ASA),
∴CN=HN=1,
∴
| k |
| a |
由MN=
| ||
| a |
| ||
| a |
整理得:a2-2a-1=0,
解得:a=
2±2
| ||
| 2 |
| 2 |
∴点C的坐标为(0,
| 2 |
则结论正确的为①③④,
故答案为:①③④
点评:此题属于反比例函数综合题,涉及的知识有:坐标与图形性质,全等三角形的判定与性质,勾股定理,以及反比例函数的性质,熟练掌握性质及定理是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,则正五边形的边长与正六边形的边长之比为( )
如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,则正五边形的边长与正六边形的边长之比为( )| A、6:5 | B、5:11 |
| C、5:6 | D、1:1 |
 如图,沪闵公路上A、B两地相距6km,C、D为两个小区,DA⊥AB,CB⊥AB,垂足分别为点A、B,已知DA长2km,CB长3km,现要在公路AB上建一个大卖场E,使得C、D两个小区到大卖场E的距离相等.
如图,沪闵公路上A、B两地相距6km,C、D为两个小区,DA⊥AB,CB⊥AB,垂足分别为点A、B,已知DA长2km,CB长3km,现要在公路AB上建一个大卖场E,使得C、D两个小区到大卖场E的距离相等. 已知:△ABC,用刻度尺量出△ABC的各边的长度,并取各边的中点,画出△ABC的三条中线,你发现了什么?
已知:△ABC,用刻度尺量出△ABC的各边的长度,并取各边的中点,画出△ABC的三条中线,你发现了什么?