Question

13．一艘轮船在A处测得北偏西75°有一灯塔P，向西航行10海里后到达B处，测得灯塔P在北偏西60°，如果轮船航向不变，那么灯塔P与轮船之间的最近距离是多少？

Answer 1

分析 过点P作PD⊥AB于点D，则直角△APD和直角△BPD有公共边PD，在两个直角三角形中，利用三角函数即可用PD表示出AD与BD，根据AB=AD-BD列方程，从而求得PD的长，即为所求．

解答 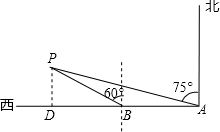解：如图，过点P作PD⊥AB于点D．
∵在直角△APD中，∠APD=75°，
∴AD=PD•tan75°=（2+$\sqrt{3}$）PD．
∵在直角△BPD中，∠BPD=60°，
∴BD=PD•tan60°=$\sqrt{3}$PD．
∵AB=AD-BD，
∴10=（2+$\sqrt{3}$）PD-$\sqrt{3}$PD，
∴PD=5．
故如果轮船航向不变，那么灯塔P与轮船之间的最近距离是5海里．

点评 本题考查了解直角三角形的应用-方向角问题，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．