Question

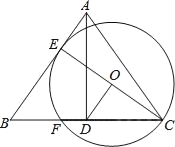
【题目】在△ABC中，已知AB＝2，∠B＝30°，AC＝．则S△ABC＝_________.

Answer 1

【答案】或

【解析】

分△ABC是锐角三角形与钝角三角形两种情况进行讨论，然后分别解直角△ABD与直角△ACD，求出AD、BD、CD的长，再根据S△ABC=BCAD，代入数值计算即可．

当△ABC是锐角三角形时，

过点A作AD⊥BC于点D，

∵AB=2，∠B=30°，

∴AD=AB=1，

∴由勾股定理可知：BD=，

∵AC=，

∴由勾股定理可知：CD=，

∴BC=BD+DC=+1，

∴S△ABC=BCAD=×（+1）×1=；

当△ABC是钝角三角形时，

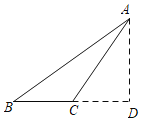
同理可得：BD=，CD=1，

∴BC=BD-DC=-1，

∴S△ABC=BCAD=×（-1）×1=．

故答案为：或 ．