题目内容
10.(1)解方程:$\frac{x}{x-2}$-$\frac{1}{x+2}$=1;(2)解不等式组:$\left\{\begin{array}{l}x-4≤0\\ \frac{x-1}{3}>\frac{1}{2}\end{array}$.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)去分母得:x2+2x-x+2=x2-4,
移项合并得:x=-6,
经检验x=-6是分式方程的解;
(2)$\left\{\begin{array}{l}{x-4≤0①}\\{\frac{x-1}{3}>\frac{1}{2}②}\end{array}\right.$,
由①得:x≤4,
由②得:x>$\frac{5}{2}$,
则不等式组的解集为$\frac{5}{2}$<x≤4.
点评 此题考查了解分式方程,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
18. 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )
象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )
 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )
象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )| A. | (-3,3) | B. | (3,2) | C. | (0,3) | D. | (1,3) |
5.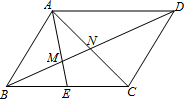 如图,在?ABCD中,E为BC的中点,连接AE、AC,分别交BD于M、N,则BM:DN等于( )
如图,在?ABCD中,E为BC的中点,连接AE、AC,分别交BD于M、N,则BM:DN等于( )
 如图,在?ABCD中,E为BC的中点,连接AE、AC,分别交BD于M、N,则BM:DN等于( )
如图,在?ABCD中,E为BC的中点,连接AE、AC,分别交BD于M、N,则BM:DN等于( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 以上都不正确 |
 如图,矩形ABCD中,tan∠BAC=$\frac{1}{2}$,点E在AB上,点F在CD上,点G、H在对角线AC上,若四边形EGFH是菱形,且EH∥BC,则AG:GH:HC=3:2:3.
如图,矩形ABCD中,tan∠BAC=$\frac{1}{2}$,点E在AB上,点F在CD上,点G、H在对角线AC上,若四边形EGFH是菱形,且EH∥BC,则AG:GH:HC=3:2:3.