题目内容
14．已知三角形ABC的三个顶点坐标分别是A（-4，-1），B（-1，4），C（1，1），点A经过平移后对应点为A1（-2，1），将三角形ABC作同样的平移得到三角形A1B1C1，写出B1、C1两点的坐标．分析 根据点A（-4，-1）经平移后对应点为A1（-2，1），得出平移变换的规律即可得出B1、C1两点的坐标
解答 解：∵点A（-4，-1）平移后点A1的坐标为（-2，1），
∴平移规律为横坐标加2，纵坐标加2，
∵B（-1，4），C（1，1），
∴B1（1，6），C1（3，3）．
点评 此题主要考查了坐标与图形的变化，关键是掌握横坐标，右移加，左移减；纵坐标，上移加，下移减．
练习册系列答案
相关题目
5．如果|3x-2|=2-3x，那么x的取值范围是（ ）
| A． | =$\frac{2}{3}$ | B． | ＞$\frac{2}{3}$ | C． | ≤$\frac{2}{3}$ | D． | ≥$\frac{2}{3}$ |
2．
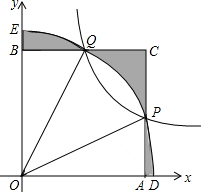如图，反比例函数y=$\frac{k}{x}$（x＞0）图象上一点P（$\sqrt{3}$，1），以点O为圆心，OP长为半径的圆弧交x轴、y轴于D、E两点，交反比例函数的图象于点Q．过点P，Q分别作x轴、y轴的垂线，交于点C，垂足为A，B，则图中阴影部分的面积为（ ）
如图，反比例函数y=$\frac{k}{x}$（x＞0）图象上一点P（$\sqrt{3}$，1），以点O为圆心，OP长为半径的圆弧交x轴、y轴于D、E两点，交反比例函数的图象于点Q．过点P，Q分别作x轴、y轴的垂线，交于点C，垂足为A，B，则图中阴影部分的面积为（ ）| A． | 3+$\frac{π}{6}$-2$\sqrt{3}$ | B． | 3+$\frac{π}{3}$-2$\sqrt{3}$ | C． | 3+$\frac{π}{6}$-$\sqrt{3}$ | D． | 3+$\frac{π}{3}$-$\sqrt{3}$ |
9．如果一个角的补角是120°，那么这个角的余角的度数是（ ）
| A． | 60° | B． | 30° | C． | 90° | D． | 120° |