题目内容
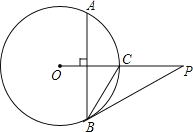
【题目】在![]() 中,
中,![]() ,
,![]() 是
是![]() 边的中线,
边的中线,![]() 于
于![]() ,连结
,连结![]() ,点
,点![]() 在射线
在射线![]() 上(与
上(与![]() ,
,![]() 不重合)
不重合)
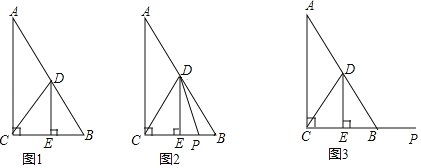
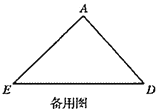
(1)如果![]()
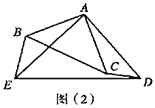
①如图1,![]()
![]()
②如图2,点![]() 在线段
在线段![]() 上,连结
上,连结![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到线段
,得到线段![]() ,连结
,连结![]() ,补全图2猜想
,补全图2猜想![]() 、
、![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
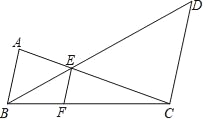
(2)如图3,若点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() span>,连结
span>,连结![]() ,将线段
,将线段![]() 绕点逆时针旋转
绕点逆时针旋转![]() 得到线段
得到线段![]() ,连结
,连结![]() ,请直接写出
,请直接写出![]() 、
、![]() 、
、![]() 三者的数量关系(不需证明)
三者的数量关系(不需证明)
【答案】(1)①60;②![]() .理由见解析;(2)
.理由见解析;(2)![]() ,理由见解析.
,理由见解析.
【解析】
(1)①根据直角三角形斜边中线的性质,结合![]() ,只要证明
,只要证明![]() 是等边三角形即可;
是等边三角形即可;
②根据全等三角形的判定推出![]() ,根据全等的性质得出
,根据全等的性质得出![]() ,
,
(2)如图2,求出![]() ,
,![]() ,求出
,求出![]() ,
,![]() ,根据全等三角形的判定得出
,根据全等三角形的判定得出![]() ,求出
,求出![]() ,推出
,推出![]() ,解直角三角形求出
,解直角三角形求出![]() 即可.
即可.
解:(1)①∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() .
.
故答案为60.
②如图1,结论:![]() .理由如下:
.理由如下:
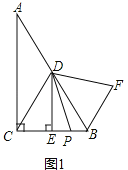
∵![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中
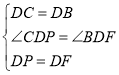 ,
,
∴![]() ,
,
∴![]() .
.
(2)结论:![]() .
.
理由:∵![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中
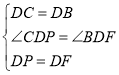 ,
,
∴![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目