Question

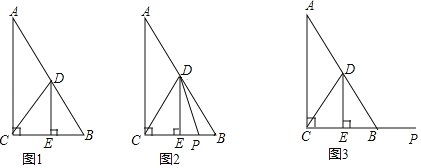
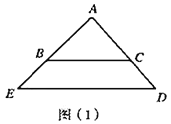
【题目】(1)问题发现：

如图（1），和都是等腰直角三角形，，点在线段上，点在线段上，请直接写出线段与的数量关系：______；（直接填写结果）

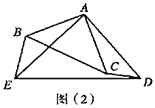
(2)操作探究：

如图（2），将图中的绕点顺时针旋转（），I小题中线段与线段的数量关系是否成立？如果不成立，说明理由，如果成立，请你结合图（2）给出的情形进行证明；

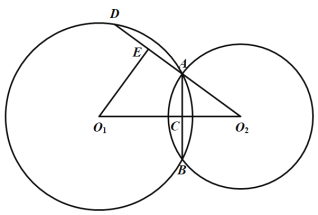
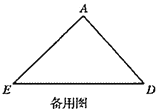
(3)解决问题：

将图（1）中的绕点顺时针旋转，若，在备用图中画出旋转图形，并判断以、、、四个点为顶点的四边形的形状.（不写证明过程）

Answer 1

【答案】（1）；（2）（1）中结论仍成立；（3）详见解析

【解析】

（1）根据等腰直角三角形的性质可得AB＝AC，AE＝AD，再根据等量关系可得线段BE与线段CD的关系；

（2）根据等腰直角三角形的性质可得AB＝AC，AE＝AD，根据旋转的性质可得∠BAE＝∠CAD，根据SAS可证△BAE≌△CAD，根据全等三角形的性质即可求解；

（3）根据题意作图，根据等腰三角形及旋转的特点证明即可求解．

（1）∵△ABC和△AED都是等腰直角三角形，∠BAC＝∠EAD＝90°，

∴AB＝AC，AE＝AD，

∴AEAB＝ADAC，

∴BE＝CD；

（2）（1）中结论仍成立，理由：

∵和都是等腰直角三角形，，

，，

由旋转的性质得，，

在与中，，

∴

∴.

（3）画图如下：

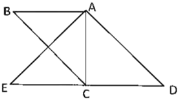
∵，△AED是等腰直角三角形，

∴AC=CD,AC⊥DE

又∵△ABC是等腰直角三角形，

∴AB=AC=CD,AB⊥AC

∴

则以、、、四点为顶点的四边形是平行四边形.