题目内容
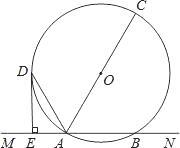
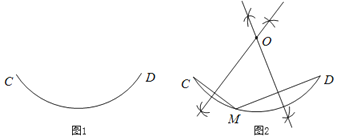
【题目】在数学课上，老师提出如下问题：尺规作图：确定图1中
所在圆的圆心．
已知：．
求作：所在圆的圆心
．
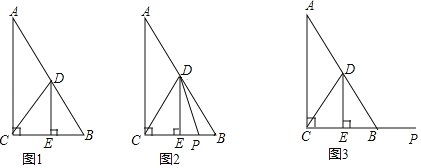
曈曈的作法如下：如图2，
（1）在上任意取一点
，分别连接
，
；
（2）分别作弦，的垂直平分线，两条垂直平分线交于点．点就是所在圆的圆心．
老师说：“曈曈的作法正确．”
请你回答：曈曈的作图依据是_____．
【答案】①线段垂直平分线上的点到线段两端点的距离相等②圆的定义（到定点的距离等于定长的点的轨迹是圆）
【解析】
（1）在
上任意取一点
，分别连接
，
；
（2）分别作弦，的垂直平分线，两条垂直平分线交于点
．点就是所在圆的圆心．
解：根据线段的垂直平分线的性质定理可知：
，
所以点是所在圆的圆心（理由①线段垂直平分线上的点到线段两端点的距离相等②圆的定义（到定点的距离等于定长的点的轨迹是圆）：）
故答案为①线段垂直平分线上的点到线段两端点的距离相等②圆的定义（到定点的距离等于定长的点的轨迹是圆）
练习册系列答案
步步高达标卷系列答案
相关题目
span>，连结
