题目内容
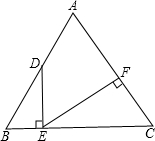 等边△ABC边长为8,D为AB边上一动点,过点D作DE⊥BC于点E,过点E作EF⊥AC于点F.
等边△ABC边长为8,D为AB边上一动点,过点D作DE⊥BC于点E,过点E作EF⊥AC于点F.
(1)若AD=2,求AF的长;
(2)求当AD取何值时,DE=EF.
解:(1)∵AB=8,AD=2
∴BD=AB-AD=6
在Rt△BDE中
∠BDE=90°-∠B=30°
∴BE= BD=3
BD=3
∴CE=BC-BE=5
在Rt△CFE中
∠CEF=90°-∠C=30°
∴CF= CE=
CE=
∴AF=AC-FC= ;
;
(2)在△BDE和△EFC中
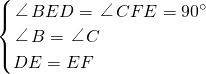 ,
,
∴△BDE≌△CFE(AAS)
∴BE=CF
∴BE=CF= EC
EC
∴BE= BC=
BC=
∴BD=2BE=
∴AD=AB-BD=
∴AD= 时,DE=EF.
时,DE=EF.
分析:(1)因为AB=8,AD=2,所以BD=AB-AD=6,又因为在Rt△BDE中∠BDE=90°-∠B=30°,根据直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半可得BE= BD=3,所以CE=BC-BE=5,同理可知,在Rt△CFE中∠CEF=90°-∠C=30°,CF=
BD=3,所以CE=BC-BE=5,同理可知,在Rt△CFE中∠CEF=90°-∠C=30°,CF= CE=
CE= ,则可根据AF=AC-FC求得结果;
,则可根据AF=AC-FC求得结果;
(2)因为∠BDE=∠CFE=90°,∠B=∠C,DE=EF,所以△BDE≌△CFE,则有BE=CF= EC,BE=
EC,BE= BC=
BC= ,BD=2BE=
,BD=2BE= ,则有AD=AB-BD=
,则有AD=AB-BD= 时,DE=EF.
时,DE=EF.
点评:本题把全等三角形的判定和性质结合求解,考查学生综合运用数学知识的能力.充分掌握和理解直角三角形中的一些特殊的对应关系并灵活运用可解得此题.
∴BD=AB-AD=6
在Rt△BDE中
∠BDE=90°-∠B=30°
∴BE=
 BD=3
BD=3∴CE=BC-BE=5
在Rt△CFE中
∠CEF=90°-∠C=30°
∴CF=
 CE=
CE=
∴AF=AC-FC=
 ;
;(2)在△BDE和△EFC中
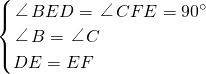 ,
,∴△BDE≌△CFE(AAS)
∴BE=CF
∴BE=CF=
 EC
EC∴BE=
 BC=
BC=
∴BD=2BE=

∴AD=AB-BD=

∴AD=
 时,DE=EF.
时,DE=EF.分析:(1)因为AB=8,AD=2,所以BD=AB-AD=6,又因为在Rt△BDE中∠BDE=90°-∠B=30°,根据直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半可得BE=
 BD=3,所以CE=BC-BE=5,同理可知,在Rt△CFE中∠CEF=90°-∠C=30°,CF=
BD=3,所以CE=BC-BE=5,同理可知,在Rt△CFE中∠CEF=90°-∠C=30°,CF= CE=
CE= ,则可根据AF=AC-FC求得结果;
,则可根据AF=AC-FC求得结果;(2)因为∠BDE=∠CFE=90°,∠B=∠C,DE=EF,所以△BDE≌△CFE,则有BE=CF=
 EC,BE=
EC,BE= BC=
BC= ,BD=2BE=
,BD=2BE= ,则有AD=AB-BD=
,则有AD=AB-BD= 时,DE=EF.
时,DE=EF.点评:本题把全等三角形的判定和性质结合求解,考查学生综合运用数学知识的能力.充分掌握和理解直角三角形中的一些特殊的对应关系并灵活运用可解得此题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
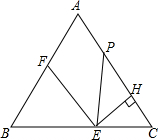 如图,等边△ABC边长为4,E是边BC上动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE=EB.设EC=x(0<x≤2).
如图,等边△ABC边长为4,E是边BC上动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE=EB.设EC=x(0<x≤2). 7、如图,等边△ABC边长为3cm,将△ABC沿AC向右平移1cm,得到△DEF,则四边形ABEF的周长( )
7、如图,等边△ABC边长为3cm,将△ABC沿AC向右平移1cm,得到△DEF,则四边形ABEF的周长( ) 14、如图,已知等边△ABC边长为1,D是△ABC外一点且∠BDC=120°,BD=CD,∠MDN=60°.
14、如图,已知等边△ABC边长为1,D是△ABC外一点且∠BDC=120°,BD=CD,∠MDN=60°. 如图,等边△ABC边长为10cm,以AB为直径的⊙O分别交CA、CB于D、E两点,则图中阴影部分的面积(结果保留π)是
如图,等边△ABC边长为10cm,以AB为直径的⊙O分别交CA、CB于D、E两点,则图中阴影部分的面积(结果保留π)是