题目内容
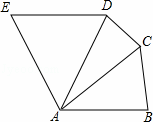
如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M为⊙O上一点,并且∠BMC=60°.
(1)求证:AB是⊙O的切线;
(2)若E,F分别是边AB,AC上的两个动点,且∠EDF=120°,⊙O的半径为2,试问BE+CF的值是否为定值?若是,求出这个定值;若不是,请说明理由.
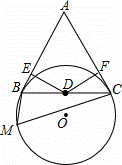
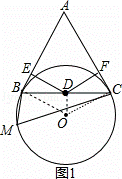
(1)证明:连结OB、OD,如图1,
∵D为BC的中点,
∴OD⊥BC,∠BOD=∠COD,
∴∠ODB=90°,
∵∠BMC=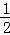 ∠BOC,
∠BOC,
∴∠BOD=∠M=60°,
∴∠OBD=30°,
∵△ABC为正三角形,
∴∠ABC=60°,
∴∠ABO=60°+30°=90°,
∴AB⊥OB,
∴AB是⊙O的切线;
(2)解:BE+CF的值是为定值.
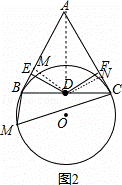
作DM⊥AB于M,DN⊥AC于N,连结AD,如图2,
∵△ABC为正三角形,D为BC的中点,
∴AD平分∠BAC,∠BAC=60°,
∴DM=DN,∠MDN=120°,
∵∠EDF=120°,
∴∠MDE=∠NDF,
在△DME和△DNF中,
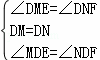 ,
,
∴△DME≌△DNF,
∴ME=NF,
∴BE+CF=BM﹣EM+CN+NF=BM+CN,
在Rt△DMB中,∵∠DBM=60°,
∴BM=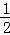 BD,
BD,
同理可得CN=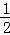 OC,
OC,
∴BE+CF=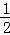 OB+
OB+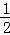 OC=
OC=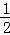 BC,
BC,
∴BE+CF的值是定值,为等边△ABC边长的一半.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
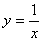 的交点,且AP=2AB,则满足条件的点P的个数是( )
的交点,且AP=2AB,则满足条件的点P的个数是( )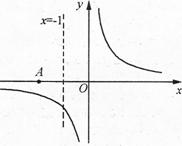
 |+
|+ ÷
÷ .
. 所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D= .
所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D= .

 个球除颜色外都相同,任意摸出一个
个球除颜色外都相同,任意摸出一个 球是黑球的概
球是黑球的概 ,那么袋中的黑球有 个.
,那么袋中的黑球有 个.