题目内容
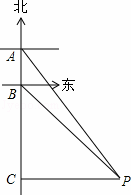
如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.
(1)求证:AM=AC;
(2)若AC=3,求MC的长.

(1)证明:连接OA,
∵AM是⊙O的切线,∴∠OAM=90°,
∵∠B=60°,∴∠AOC=120°,
∵OA=OC,∴∠OCA=∠OAC=30°,
∴∠AOM=60°,∴∠M=30°,
∴∠OCA=∠M,
∴AM=AC;
(2)作AG⊥CM于G,
∵∠OCA=30°,AC=3,∴AG= ,
,
由勾股定理的,CG= ,
,
则MC=2CG=3 .
.


点评: 本题考查的是切线是性质、等腰三角形的性质和勾股定理的应用,掌握圆的切线垂

练习册系列答案
相关题目
 +(π﹣2015)0﹣|
+(π﹣2015)0﹣| ﹣2|+2sin60°.
﹣2|+2sin60°. =( )
=( ) . ﹣2 C. 2 D. 2
. ﹣2 C. 2 D. 2
 B. 10
B. 10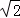 ﹣10 C. 10 D. 10
﹣10 C. 10 D. 10 C.﹣0.5 D.1
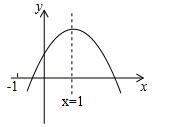
C.﹣0.5 D.1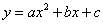 的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a=b,④4a+2b+c>0,⑤若点(﹣2,
的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a=b,④4a+2b+c>0,⑤若点(﹣2,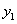 )和(
)和( ,
,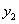 )在该
)在该 图象上,则
图象上,则 .其中正确的
.其中正确的