题目内容
20.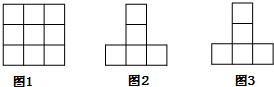 将一些棱长为1的正方体摆放在3×3的平面上(如图1所示),其正视图和侧视图分别如图2、图3,记摆放的正方体个数的最大值为m,最小值为n,则m-n=( )
将一些棱长为1的正方体摆放在3×3的平面上(如图1所示),其正视图和侧视图分别如图2、图3,记摆放的正方体个数的最大值为m,最小值为n,则m-n=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 根据正视图和侧视图,即可确定摆放的正方体个数的最大值m和最小值n的值,进而求出m-n的值.
解答  解:由三视图可知,要满足正视图和侧视图的条件,
解:由三视图可知,要满足正视图和侧视图的条件,
则最大值为m=11,最小值为n=5,
所以m-n=11-5=6.
故选C.
点评 本题考查对三视图的理解应用及空间想象能力.只要掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就很容易得到答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列表述中,能确定准确位置的是( )
| A. | 教室第三排 | B. | 湖南东路 | ||
| C. | 南偏东40° | D. | 东经112°,北纬51° |
15. 2015年元旦前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
2015年元旦前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)若用w(元)表示工艺厂试销该工艺品每天获得的利润,试求w(元)与x(元)之间的函数关系式.
(3)若该工艺品的每天的总成本不能超过2500元,那么销售单价定为多少时,工艺厂试销工艺品每天获得的利润最大,最大是多少元?
 2015年元旦前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
2015年元旦前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过调查,得到如下数据:| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量y(件) | … | 500 | 400 | 300 | 200 | 100 | … |
(2)若用w(元)表示工艺厂试销该工艺品每天获得的利润,试求w(元)与x(元)之间的函数关系式.
(3)若该工艺品的每天的总成本不能超过2500元,那么销售单价定为多少时,工艺厂试销工艺品每天获得的利润最大,最大是多少元?
5.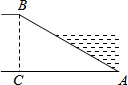 如图,河坝横断面迎水坡AB的坡比是1:$\sqrt{3}$(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3m,则坡面AB的长度是( )
如图,河坝横断面迎水坡AB的坡比是1:$\sqrt{3}$(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3m,则坡面AB的长度是( )
 如图,河坝横断面迎水坡AB的坡比是1:$\sqrt{3}$(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3m,则坡面AB的长度是( )
如图,河坝横断面迎水坡AB的坡比是1:$\sqrt{3}$(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3m,则坡面AB的长度是( )| A. | 9m | B. | 6m | C. | 6$\sqrt{3}$m | D. | 3$\sqrt{3}$m |
12.填在下面各正方形中的四个数之间都有相同的规律,根据这种规律m的值应是( )

| A. | 110 | B. | 168 | C. | 212 | D. | 222 |
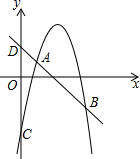 已知:抛物线y=-x2+bx+c的图象交y轴于点C,一次函数y=-x+m交y轴于点D,交抛物线于A、B两点,B(6,-3),且AB=2AD.
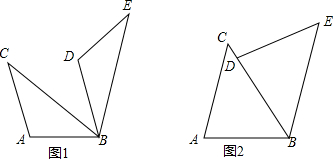
已知:抛物线y=-x2+bx+c的图象交y轴于点C,一次函数y=-x+m交y轴于点D,交抛物线于A、B两点,B(6,-3),且AB=2AD.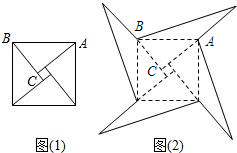 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )
如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )