题目内容
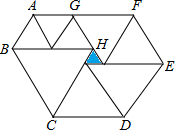 如图,是由9个等边三角形(三条边都相等的三角形)组成的装饰图案,已知中间最小的等边三角形(阴影部分)边长为2cm,则多边形ABCDEFG的周长是
如图,是由9个等边三角形(三条边都相等的三角形)组成的装饰图案,已知中间最小的等边三角形(阴影部分)边长为2cm,则多边形ABCDEFG的周长是考点:一元一次方程的应用
专题:几何图形问题
分析:设△ABM与△GMH的边长为xcm,根据图形中等边三角形的关系列出关于x的方程,求出方程的解得到x的值,即可确定出多边形ABCDEF的周长.
解答: 解:设△ABM与△GMH的边长为xcm,
解:设△ABM与△GMH的边长为xcm,
则△GNF与△EFN的边长为(x+2)cm,△DEP与△CDP的边长为(x+4)cm,△BCH的边长为(x+6)cm,
∴AB=AG=xcm,FG=EF=(x+2)cm,DE=CD=(x+4)cm,BC=(x+6)cm,
根据题意得:BH=BM+MH=2BM,即x+6=2x,
解得:x=6,
则多边形ABCDEF的周长为2x+x+2+x+2+x+4+x+4+x+6=7x+18=60cm.
故答案为:60
 解:设△ABM与△GMH的边长为xcm,
解:设△ABM与△GMH的边长为xcm,则△GNF与△EFN的边长为(x+2)cm,△DEP与△CDP的边长为(x+4)cm,△BCH的边长为(x+6)cm,
∴AB=AG=xcm,FG=EF=(x+2)cm,DE=CD=(x+4)cm,BC=(x+6)cm,
根据题意得:BH=BM+MH=2BM,即x+6=2x,
解得:x=6,
则多边形ABCDEF的周长为2x+x+2+x+2+x+4+x+4+x+6=7x+18=60cm.
故答案为:60
点评:此题考查了一元一次方程的应用,找出题中的等量关系是解本题的关键.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
若3x3-x=1,则9x4+12x3-3x2-7x+2001的值等于( )
| A、1999 | B、2001 |
| C、2003 | D、2005 |
下列说法正确的是( )
| A、0是最小的整数 |
| B、0没有相反数 |
| C、1是最小的自然数 |
| D、-1是最大的负整数. |
下列说法中,正确的是( )
| A、不带根号的数不是无理数 | ||||
| B、8的立方根是±2 | ||||
C、绝对值是
| ||||
| D、每个实数都对应数轴上一个点 |
 如图,AB是⊙O的直径,D是AC的中点,OD∥BC,若AB=10,AD=4,则OD=
如图,AB是⊙O的直径,D是AC的中点,OD∥BC,若AB=10,AD=4,则OD=