题目内容
已知关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=-1,x2=2,则二次函数y=x2+mx+n中,当y<0时,x的取值范围是 .
考点:二次函数与不等式(组),抛物线与x轴的交点
专题:计算题
分析:先根据方程的解写出抛物线与x轴的交点坐标,再写出抛物线在x轴下方部分的x的取值范围即可.
解答:解:∵x2+mx+n=0的两个实数根分别为x1=-1,x2=2,
∴二次函数y=x2+mx+n与x轴的两个交点坐标分别为(-1,0),(2,0),
∵a=1>0,
∴抛物线开口向上,
∴y<0时,x的取值范围是:-1<x<2.
故答案为:-1<x<2.
∴二次函数y=x2+mx+n与x轴的两个交点坐标分别为(-1,0),(2,0),
∵a=1>0,
∴抛物线开口向上,
∴y<0时,x的取值范围是:-1<x<2.
故答案为:-1<x<2.
点评:本题考查了二次函数与不等式,抛物线与x轴的交点,熟记二次函数的性质以及函数图象的特征是解题的关键.

练习册系列答案
相关题目
数轴上表示整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为1001厘米的线段AB,则线段AB盖住的整点的个数是( )
| A、998或999 |
| B、999或1000 |
| C、1000或1001 |
| D、1001或1002 |
下列说法中正确的是( )
| A、-an和(-a)n一定是互为相反数 |
| B、当n为奇数时,-an和(-a)n相等 |
| C、当n为偶数时,-an和(-a)n相等 |
| D、-an和(-a)n一定不相等 |
一个正方形的边长增加了2cm,面积相应地增加了32cm2,则这个正方形的边长为( )cm.
| A、5 | B、6 | C、7 | D、8 |
下列语句中是命题的是( )
| A、∠A=50° |
| B、作直线⊥ab |
| C、对顶角相等吗? |
| D、延长AB到C使BC=2AB |
 如图,化简
如图,化简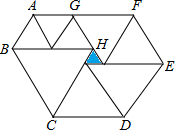 如图,是由9个等边三角形(三条边都相等的三角形)组成的装饰图案,已知中间最小的等边三角形(阴影部分)边长为2cm,则多边形ABCDEFG的周长是
如图,是由9个等边三角形(三条边都相等的三角形)组成的装饰图案,已知中间最小的等边三角形(阴影部分)边长为2cm,则多边形ABCDEFG的周长是