题目内容
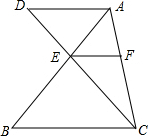如图所示，在△ABC中，AE：EB=1：2，EF∥BC，AD∥BC交CE的延长线于D，求| S△AEF |
| S△BCE |
考点：相似三角形的判定与性质
专题：
分析：如图，首先证明△AEF∽△ABC，进而证明
=(
)2=
，
=
=
，运用图形中三角形面积之间的关系，即可解决问题．
| S△AEF |
| S△ABC |
| AE |
| AB |
| 1 |
| 9 |
| S△AEF |
| S△EFC |
| AF |
| FC |
| 1 |
| 2 |
解答：解：如图，∵EF∥BC，且AE：EB=1：2，
∴
=
=
，△AEF∽△ABC，
∴
=
，
=(
)2=
，
=
=
，
设S△AEF=λ，则S△ABC=9λ，S△EFC=2λ，
∴S△BEC=6λ，
∴
=
．
解：如图，∵EF∥BC，且AE：EB=1：2，∴
| AE |
| BE |
| AF |
| FC |
| 1 |
| 2 |
∴
| AE |
| AB |
| 1 |
| 3 |
| S△AEF |
| S△ABC |
| AE |
| AB |
| 1 |
| 9 |
| S△AEF |
| S△EFC |
| AF |
| FC |
| 1 |
| 2 |
设S△AEF=λ，则S△ABC=9λ，S△EFC=2λ，
∴S△BEC=6λ，
∴
| S△AEF |
| S△BEC |
| 1 |
| 6 |
点评：该题主要考查了相似三角形的判定及其性质等几何知识点及其应用问题；牢固掌握相似三角形的判定及其性质是解题的关键．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
-8的相反数是（ ）
A、
| ||
| B、-8 | ||
| C、8 | ||
D、-
|
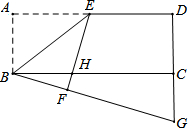已知如图，在矩形ABCD中，点E是AD的中点，连结BE，将△ABE沿着BE翻折得到△FBE，EF交BC于点H，延长BF、DC相交于点G，若DG=16，BC=24，则FH=房间窗户的边框形状是矩形，在阳光的照射下边框在房间地面上形成了投影，则投影的形状可能是（ ）
| A、三角形 | B、平行四边形 |
| C、圆 | D、梯形 |
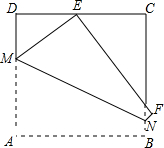如图，将边长为12cm的正方形ABCD折叠，使得A点落在边CD上的E点，然后压平得折痕MN，若MN的长为13cm，则线段NF的长为
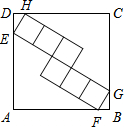如图，正方形ABCD的边长为5，内部有6个大小相同的小正方形，小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上，则小正方形的边长为