题目内容
若式子(x-y)0无意义,求[(x+2y)2-(x+y)(3x-y)-5y2]÷(2x)的值.
考点:整式的混合运算—化简求值,零指数幂
专题:
分析:根据零指数求出x=y,算乘法,合并同类项,算除法,最后代入求出即可.
解答:解:∵式子(x-y)0无意义,
∴x-y=0,
∴x=y,
∴[(x+2y)2-(x+y)(3x-y)-5y2]÷(2x)
=[x2+4xy+4y2-3x2+xy-3xy+y2-5y2]÷(2x)
=[-2x2+2xy]÷2x
=-x+y
=0.
∴x-y=0,
∴x=y,
∴[(x+2y)2-(x+y)(3x-y)-5y2]÷(2x)
=[x2+4xy+4y2-3x2+xy-3xy+y2-5y2]÷(2x)
=[-2x2+2xy]÷2x
=-x+y
=0.
点评:本题考查了整式的混合运算和求值,零指数幂的应用,主要考查学生的计算和化简能力,难度适中.

练习册系列答案
相关题目
下列计算中,正确的是( )
| A、(-1)2×(-1)5=1 | ||||
B、-3÷(-
| ||||
C、
| ||||
| D、-(-3)2=9 |
发射一枚炮弹,经x秒后的高度为y公尺,且时间与高度关系为y=ax2+bx,若此炮弹在第10秒与第20秒时的高度相等,则下列四个时间中,哪一个时间炮弹的高度是最高的?( )
| A、第9秒 | B、第13秒 |
| C、第15秒 | D、第18秒 |
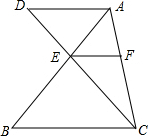 如图所示,在△ABC中,AE:EB=1:2,EF∥BC,AD∥BC交CE的延长线于D,求
如图所示,在△ABC中,AE:EB=1:2,EF∥BC,AD∥BC交CE的延长线于D,求