题目内容
某童装厂现有甲种布料38米,乙种布料26米.现计划用这两种布料生产L、M两种型号的童装50套.已知做一套L型号的童装需甲种布料0.5米,乙种布料1米,可获利45元.做一套M型号的童装需甲种布料0.9米.乙种布料0.2米,可获利30元.
(1)按要求安排L、M两种型号的童装的生产件数,有哪几种方案?请你设计出来;
(2)在你设计的方案中,哪种生产方案获总利润最大?最大利润是多少?
(1)按要求安排L、M两种型号的童装的生产件数,有哪几种方案?请你设计出来;
(2)在你设计的方案中,哪种生产方案获总利润最大?最大利润是多少?
考点:一次函数的应用,一元一次不等式组的应用
专题:
分析:(1)设生产L型号童装x套,M型号童装(50-x)套,然后根据所需甲、乙两种布料不超过现有材料列出一元一次不等式组,求解后再根据x是正整数设计方案;
(2)列出获得利润的表达式,再根据一次函数的增减性求出最大利润即可.
(2)列出获得利润的表达式,再根据一次函数的增减性求出最大利润即可.
解答:解:(1)设生产L型号童装x套,M型号童装(50-x)套,
由题意得,
,
解不等式①得,x≥17.5,
解不等式②得,x≤20,
所以,不等式组的解集是17.5≤x≤20,
∵童装套数x是正整数,
∴x=18、19、20,
∴有以下三种设计方案:
方案一,生产L型号18套,M型号32套,
方案二,生产L型号19套,M型号31套,
方案三,生产L型号20套,M型号30套;
(2)设获得利润为y元,
则y=45x+30(50-x)=15x+1500,
∵k=15>0,
∴y随x的增大而增大,
∴当x=20时,y有最大值15×20+1500=1800,
即第三种生产方案,生产L型号20套,M型号30套获总利润最大,最大利润是1800元.
由题意得,
|
解不等式①得,x≥17.5,
解不等式②得,x≤20,
所以,不等式组的解集是17.5≤x≤20,
∵童装套数x是正整数,
∴x=18、19、20,
∴有以下三种设计方案:
方案一,生产L型号18套,M型号32套,
方案二,生产L型号19套,M型号31套,
方案三,生产L型号20套,M型号30套;
(2)设获得利润为y元,
则y=45x+30(50-x)=15x+1500,
∵k=15>0,
∴y随x的增大而增大,
∴当x=20时,y有最大值15×20+1500=1800,
即第三种生产方案,生产L型号20套,M型号30套获总利润最大,最大利润是1800元.
点评:本题考查了一次函数的应用,一元一次不等式组的应用,读懂题目信息,找出不等量关系列出不等式组是解题的关键,(2)利用一次函数的增减性求最值问题是常考内容,需熟练掌握并灵活运用.

练习册系列答案
相关题目
2012年伦敦奥运会上,中国选手吕小军在男子举重77公斤级比赛中,打破了原奥运会纪录,创造了新抓举纪录,成绩是175公斤,下列说法正确的是( )
| A、原来奥运会纪录是175公斤 |
| B、原来奥运会纪录是77公斤 |
| C、原来奥运会纪录小于77公斤 |
| D、原来奥运会纪录小于175公斤 |
 黄河游览区在假日一周旅游的调查中每天旅游的人数变化如表(正数表示比前一天多的人数,负数表示比前一天少的人数):
黄河游览区在假日一周旅游的调查中每天旅游的人数变化如表(正数表示比前一天多的人数,负数表示比前一天少的人数):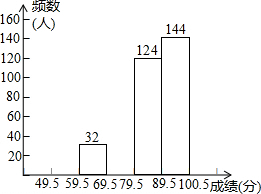 某市七年级有10000名学生参加安全应急预案知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了400名学生的得分进行统计请你根据不完整的频率分布表.解答下列问题:
某市七年级有10000名学生参加安全应急预案知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了400名学生的得分进行统计请你根据不完整的频率分布表.解答下列问题: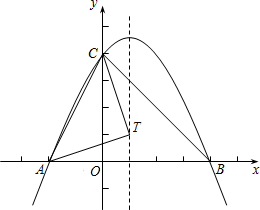 如图,抛物线y=ax2+bx+4(a≠0)与x轴交于点A(-2,0)和B(4,0)、与y轴交于点C.
如图,抛物线y=ax2+bx+4(a≠0)与x轴交于点A(-2,0)和B(4,0)、与y轴交于点C.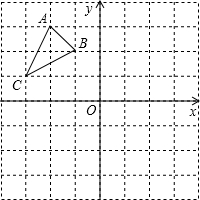 如图,在边长为1的正方形组成的网格中,△ABC的顶点均在格点上,点A、B、C的坐标分别是A(-2,3)、B(-1,2)、C(-3,1),△ABC绕点O顺时针旋转90°后得到△A1B1C1.
如图,在边长为1的正方形组成的网格中,△ABC的顶点均在格点上,点A、B、C的坐标分别是A(-2,3)、B(-1,2)、C(-3,1),△ABC绕点O顺时针旋转90°后得到△A1B1C1.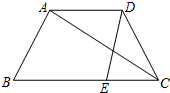 如图,已知在梯形ABCD中,AD∥BC,点E在边BC上,连接DE,AC.
如图,已知在梯形ABCD中,AD∥BC,点E在边BC上,连接DE,AC.