Question

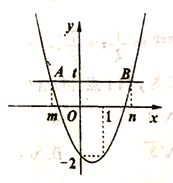
【题目】抛物线（为常数，）与轴交于，两点，与轴交于点．设该抛物线的顶点为，其对称轴与轴的交点为．

（1）求该抛物线的解析式；

（2）为线段（含端点）上一点，为轴上一点，且．

①求的取值范围；

②当取最大值时，将线段向上平移个单位长度，使得线段与抛物线有两个交点，求的取值范围．

Answer 1

【答案】（1）；（2）①；②

【解析】

（1）利用待定系数法将A和B的坐标代入求解即可；

（2）①抛物线的对称轴为：x=2，顶点M（2，4），在Rt△PCQ中，由勾股定理得：PC2+PQ2=CQ2，把三角形三边长用点P，Q的坐标表达出来，整理得：，利用0≤m≤4，求出n的取值范围；

②设线段CQ向上平移t个单位长度后的解析式为：联立抛物线方程，可求出x2-7x+4t=0，由△=49-16t=0，得，可得当线段CQ与抛物线有两个交点时，.

解：（1）∵ 点，在抛物线上，

∴

解得，．

∴ 该抛物线的解析式为；

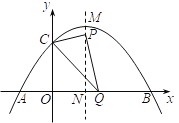
（2）① 由，得（2，4），

设点坐标为（2，m），其中，

则，，，

∵，

∴在△PCQ中，，

即，

整理得，0≤m≤4，

∴当时，取得最小值为；

当时，取得最大值为，

∴的取值范围是；

②由①知，当取最大值4时，．此时，

∵点，

∴线段的解析式为，

设向上平移个单位长度后的解析式为．

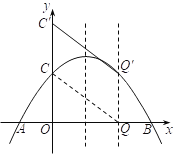
如图，当线段向上平移，使点恰好在抛物线上时，线段与抛物线有两个交点，此时点的坐标．

将代入，得．

当线段继续向上平移，线段与抛物线只有一个交点时，

由，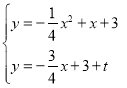

得．化简，得．

由，解得．

∴的取值范围是．