Question

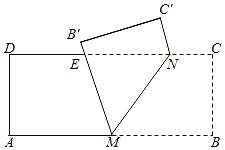
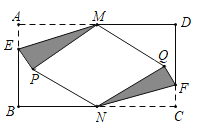
【题目】如图， 在矩形纸片中， ， 点，分别是，的中点， 点，分别在，上， 且.将沿折叠， 点的对应点为点，将沿折叠， 点的对应点为点，当四边形为菱形时， 则_______．

Answer 1

【答案】

【解析】

连接MN，PQ交于点O，延长PQ交CD于H，延长QP交AB于G．解直角三角形求出AG，EG即可解决问题．

如图，连接MN，PQ交于点O，延长PQ交CD于H，延长QP交AB于G．

∵四边形PNQM是菱形，

∴MN⊥PQ，

∵点M、N分别是AD、BC的中点，

∴AM=BN，

又∵矩形ABCD中，AM∥BN，∠A=90°，

∴四边形AMNB是矩形，

∴∠AMN=90°

∴PQ∥AD∥BC，

∴AG=DK=OM=AB=AD=1，

∵PM=AM=2，

∴sin∠MPO=，

∴∠MPO=30°，

∵∠EPM=90°，

∴∠EPG=90°-30°=60°

∴OP=OM=，

∵OG=2，

∴EG=PGtan60°=2-3，

∴GP=2-，

∴AE=AG-EG=1-（2-3）=4-2．

故答案为：4-2．