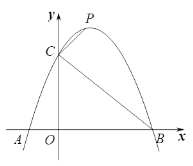题目内容
【题目】抛物线![]()
![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() .
.
(1)若![]() ,求
,求![]() ,
,![]() 满足的关系式;
满足的关系式;
(2)直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,抛物线的对称轴为直线
两点,抛物线的对称轴为直线![]() ,且
,且![]() .
.
①求抛物线的解析式(各项系数用含![]() 的式子表示);
的式子表示);
②求线段![]() 长度的取值范围.
长度的取值范围.
【答案】(1)![]() ;(2)①
;(2)①![]() ②
②![]() 或
或![]()
【解析】
(1)将点A的坐标和c=a代入到抛物线的解析中,化简即可得出a,b之间的关系式.
(2) ①由抛物线的对称轴为x=1得到a,b之间的关系,根据点A抛物线上,可求出a,c之间的关系;
②首先用含有a的式子表示出CD的长,根据正切值得范围求出a的取值范围,再结合a的取值范围求出CD的取值范围.
解:(1)若![]() ,抛物线解析式化为
,抛物线解析式化为![]() .
.
![]() 点
点![]() 在抛物线上,
在抛物线上,
![]() ,
,
![]() .
.
(2)①![]() 抛物线的对称轴为直线
抛物线的对称轴为直线![]() ,
,
![]() ,
,
![]() .
.
![]() 点
点![]() 在抛物线上,
在抛物线上,
![]() ,
,
![]() .
.
![]() 抛物线解析式化为
抛物线解析式化为![]() .
.
②![]() 直线
直线![]() 经过点
经过点![]() ,且点
,且点![]() ,
,
![]() ,
,
![]() 直线化为
直线化为![]() .
.
由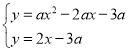 ,解得
,解得![]() ,
,![]() .
.
即![]() .
.
![]() 点
点![]() .
.
由勾股定理得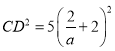
依题意可知,点![]() 在点
在点![]() 右侧,
右侧,
![]() 且
且![]() .
.
由抛物线对称性可得点![]()
![]() ,
,
![]() .
.
![]() 当
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
当![]() 时,由反比例函数性质得
时,由反比例函数性质得![]() ,
,![]() ;
;
当![]() 时,由反比例函数性质得
时,由反比例函数性质得![]() ,
,![]() ;
;
综上所述:![]() 或
或![]() .
.

练习册系列答案
相关题目