题目内容
 如图,已知双曲线y=
如图,已知双曲线y=| m | x |
(1)求两个函数的解析式;
(2)若直线与x轴交于点B,求S△BOP的值.
分析:(1)利用待定系数法分别求出反比例函数与一次函数解析式即可;
(2)利用(1)中所求一次函数解析式得出B点坐标,进而得出BO的长,即可得出S△BOP的值.
(2)利用(1)中所求一次函数解析式得出B点坐标,进而得出BO的长,即可得出S△BOP的值.
解答: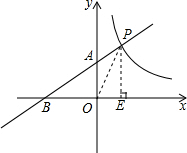 解;(1)∵双曲线y=
解;(1)∵双曲线y=
与直线y=kx+b交于第一象限点P(2,3),且直线穿过点A(0,2),
∴m=2×3=6,
,
解得:
.
∴直线解析式为:y=
x+2,双曲线解析式为:y=
;
(2)连接OP,作PE⊥x轴于点E,
∵y=
x+2=0时,x=-4,
∴直线与x轴交于点(-4,0),
∴BO=4,
∵点P(2,3),
∴PE的长为:3,
∴S△BOP=
×BO×PE=
×4×3=6.
 解;(1)∵双曲线y=
解;(1)∵双曲线y=| m |
| x |
∴m=2×3=6,
|
解得:
|
∴直线解析式为:y=
| 1 |
| 2 |
| 6 |
| x |
(2)连接OP,作PE⊥x轴于点E,
∵y=
| 1 |
| 2 |
∴直线与x轴交于点(-4,0),
∴BO=4,
∵点P(2,3),
∴PE的长为:3,
∴S△BOP=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了待定系数法求反比例函数和一次函数解析式以及三角形面积求法等知识,根据已知得出B点坐标是解题关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
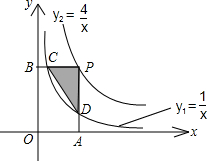 如图,已知双曲线
如图,已知双曲线 (2012•济南)如图,已知双曲线y=
(2012•济南)如图,已知双曲线y= (2013•徐州模拟)如图,已知双曲线y=
(2013•徐州模拟)如图,已知双曲线y= 如图,已知双曲线
如图,已知双曲线 如图,已知双曲线
如图,已知双曲线