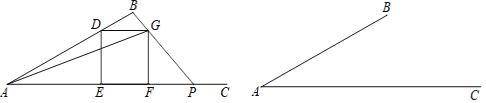
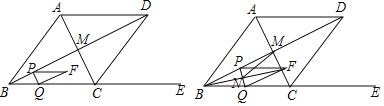
题目内容
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() (如图),点
(如图),点![]() ,
,![]() 分别为射线
分别为射线![]() 上的动点(点C、E都不与点B重合),连接AC、AE使得
上的动点(点C、E都不与点B重合),连接AC、AE使得![]() ,射线
,射线![]() 交射线
交射线![]() 于点
于点![]() ,设
,设![]() ,
,![]() .
.
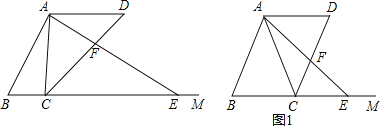
(1)如图1,当![]() 时,求AF的长.
时,求AF的长.
(2)当点![]() 在点
在点![]() 的右侧时,求
的右侧时,求![]() 关于
关于![]() 的函数关系式,并写出函数的定义域.
的函数关系式,并写出函数的定义域.
(3)连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() 是等腰三角形,直接写出
是等腰三角形,直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
过点![]() 作
作![]() 于N,利用∠B的余弦值可求出BN的长,利用勾股定理即可求出AN的长,根据线段的和差关系可得CN的长,利用勾股定理可求出AC的长,根据AD//BC,AD=BC即可证明四边形ABCD是平行四边形,可得∠B=∠D,进而可证明△ABC∽△ADF,根据相似三角形的性质即可求出AF的长;(2)根据平行线的性质可得
于N,利用∠B的余弦值可求出BN的长,利用勾股定理即可求出AN的长,根据线段的和差关系可得CN的长,利用勾股定理可求出AC的长,根据AD//BC,AD=BC即可证明四边形ABCD是平行四边形,可得∠B=∠D,进而可证明△ABC∽△ADF,根据相似三角形的性质即可求出AF的长;(2)根据平行线的性质可得![]() ,根据等量代换可得
,根据等量代换可得![]() ,进而可证明△ABC∽△ABE,根据相似三角形的性质可得
,进而可证明△ABC∽△ABE,根据相似三角形的性质可得![]() ,可用x表示出BE、CE的长,根据平行线分线段成比例定理可用x表示出
,可用x表示出BE、CE的长,根据平行线分线段成比例定理可用x表示出![]() 的值,根据
的值,根据![]() 可得y与x的关系式,根据x>0,CE>0即可确定x的取值范围;(3)分PA=PD、AP=AD和AD=PD三种情况,根据BE=
可得y与x的关系式,根据x>0,CE>0即可确定x的取值范围;(3)分PA=PD、AP=AD和AD=PD三种情况,根据BE=![]() 及线段的和差关系,分别利用勾股定理列方程求出x的值即可得答案.
及线段的和差关系,分别利用勾股定理列方程求出x的值即可得答案.
(1)如图,过点![]() 作
作![]() 于N,
于N,
∵AB=5,![]() ,
,
∴在![]() 中,
中,![]() =5×
=5×![]() =3,
=3,
∴AN=![]() =
=![]() =4,
=4,
∵BC=x=4,
∴CN=BC-BN=4-3=1,
在![]() 中,
中,![]() ,
,
∵AD=4,BC=x=4,
∴AD=BC,
∵![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
又∵![]() ,
,
∴△ABC∽△ADF,
∴![]() ,
,
∴![]()
解得:![]() ,
,
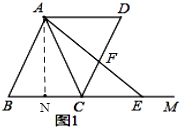
(2)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵∠B=∠B,
∴△ABC∽△ABE,
∴![]() ,
,
∴![]() ,
,
∵AD//BC,
∴![]() ,
,
∴![]() ,
,
∵x>0,CE=![]() >0,
>0,
∴0<x<5,
∴![]() ,
,
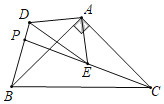
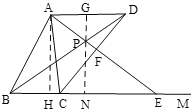
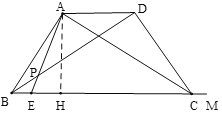
(3)①如图,当PA=PD时,作AH⊥BM于H,PG⊥AD于G,延长GP交BM于N,
∵PA=PD,AD=4,
∴AG=DG=2,∠ADB=∠DAE,
∵AD//BE,
∴GN⊥BE,∠DAE=∠AEB,∠ADB=∠DBE,
∴∠DBE=∠AEB,
∴PB=PE,
∴BN=EN=![]() BE=
BE=![]() ,
,
∵![]() ,AB=5,
,AB=5,
∴BH=AB·cos∠ABH=3,
∵AH⊥BM,GN⊥MB,GN⊥AD,
∴∠AHN=∠GNH=∠NGA=90°,
∴四边形AHNG是矩形,
∴HN=AG=2,
∴BN=BH+HN=3+2=5,
∴![]() =5,
=5,
解得:x=![]() .
.
②如图,当AP=AD=4时,作AH⊥BM于H,
∴∠ADB=∠APD,
∵AD//BM,
∴∠ADB=∠DBC,
∵∠APD=∠BPE,
∴∠DBC=∠BPE,
∴BE=PE=![]() ,
,
∵cos∠ABC=![]() ,AB=5,
,AB=5,
∴BH=3,AH=4,
∴在Rt△AEH中,(4+![]() )2=42+(3-
)2=42+(3-![]() )2,
)2,
解得:x=![]() ,
,
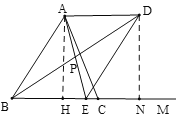
③如图,当AD=PD=4时,作AH⊥BM于H,DN⊥BM于N,
∴∠DAP=∠DPA,
∵AD//BM,
∴∠DAP=∠AEB,
∵∠APD=∠BPE,
∴∠BPE=∠AEB,
∴BP=BE=![]() ,
,
∵cos∠ABC=![]() ,AB=5,
,AB=5,
∴BH=3,AH=4,
∵AD//BM,AH⊥BM,DN⊥BM,
∴四边形AHND是矩形,
∴DN=AH=4,HN=AD=4,
中Rt△BND中,(4+![]() )2=42+(4+3)2,
)2=42+(4+3)2,
解得:x=![]() ,
,
综上所述:x的值为![]() 或
或![]() 或
或![]() .
.

 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案【题目】为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据:
(1)由上表填空:a= ,b= ,c= ,d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.