题目内容
【题目】如图,在菱形ABCD中,对角线AC与BD相交于点M,已知BC=5,点E在射线BC上,tan∠DCE=![]() ,点P从点B出发,以每秒2
,点P从点B出发,以每秒2![]() 个单位沿BD方向向终点D匀速运动,过点P作PQ⊥BD交射线BC于点O,以BP、BQ为邻边构造PBQF,设点P的运动时间为t(t>0).
个单位沿BD方向向终点D匀速运动,过点P作PQ⊥BD交射线BC于点O,以BP、BQ为邻边构造PBQF,设点P的运动时间为t(t>0).
(1)tan∠DBE= ;
(2)求点F落在CD上时t的值;
(3)求PBQF与△BCD重叠部分面积S与t之间的函数关系式;
(4)连接PBQF的对角线BF,设BF与PQ交于点N,连接MN,当MN与△ABC的边平行(不重合)或垂直时,直接写出t的值.
【答案】(1)![]() ;(2)t=
;(2)t=![]() ;(3)见解析;(4)t的值为
;(3)见解析;(4)t的值为![]() 或
或![]() 或
或![]() 或2.
或2.
【解析】
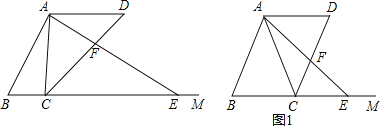
(1)如图1中,作DH⊥BE于H.解直角三角形求出BH,DH即可解决问题.
(2)如图2中,由PF∥CB,可得![]() ,由此构建方程即可解决问题.
,由此构建方程即可解决问题.
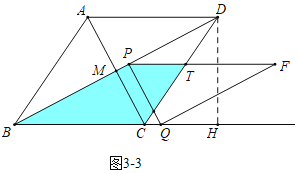
(3)分三种情形:如图3-1中,当![]() 时,重叠部分是平行四边形PBQF.如图3-2中,当
时,重叠部分是平行四边形PBQF.如图3-2中,当![]() 时,重叠部分是五边形PBQRT.如图3-3中,当1<t≤2时,重叠部分是四边形PBCT,分别求解即可解决问题.
时,重叠部分是五边形PBQRT.如图3-3中,当1<t≤2时,重叠部分是四边形PBCT,分别求解即可解决问题.
(4)分四种情形:如图4-1中,当MN∥AB时,设CM交BF于T.如图4-2中,当MN⊥BC时.如图4-3中,当MN⊥AB时.当点P与点D重合时,MN∥BC,分别求解即可.
解:(1)如图1中,作DH⊥BE于H.
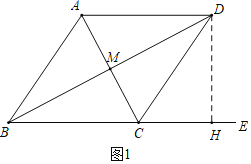
在Rt△BCD中,∵∠DHC=90°,CD=5,tan∠DCH=![]() ,
,
∴DH=4,CH=3,
∴BH=BC+CH=5+3=8,
∴tan∠DBE=![]() =
=![]() =
=![]() .
.
故答案为![]() .
.
(2)如图2中,
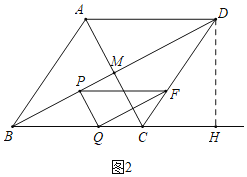
∵四边形ABCD是菱形,
∴AC⊥BD,
∵BC=5,tan∠CBM=![]() =
=![]() ,
,
∴CM=![]() ,BM=DM=2
,BM=DM=2![]() ,
,
∵PF∥CB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得t=![]() .
.
(3)如图3﹣1中,当0<t≤![]() 时,重叠部分是平行四边形PBQF,S=PBPQ=2
时,重叠部分是平行四边形PBQF,S=PBPQ=2![]() t
t![]() t=10t2.
t=10t2.
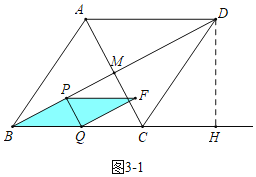
如图3﹣2中,当![]() <t≤1时,重叠部分是五边形PBQRT,S=S平行四边形PBQF﹣S△TRF=10t2﹣
<t≤1时,重叠部分是五边形PBQRT,S=S平行四边形PBQF﹣S△TRF=10t2﹣![]() [2
[2![]() t﹣(5﹣5t)]
t﹣(5﹣5t)]![]() [2
[2![]() t﹣(5﹣5t)]=﹣55t2+(20
t﹣(5﹣5t)]=﹣55t2+(20![]() +50)t﹣25.
+50)t﹣25.
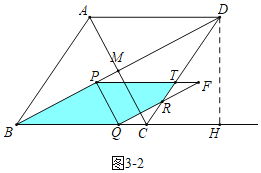
如图3﹣3中,当1<t≤2时,重叠部分是四边形PBCT,S=S△BCD﹣S△PDT=![]() ×5×4﹣
×5×4﹣![]() (5﹣
(5﹣![]() t)(4﹣2t)=﹣
t)(4﹣2t)=﹣![]() t2+10t.
t2+10t.
(4)如图4﹣1中,当MN∥AB时,设CM交BF于T.

∵PN∥MT,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴MT=![]() ,
,
∵MN∥AB,
∴![]() =
=![]() =
=![]() =2,
=2,
∴PB=![]() BM,
BM,
∴2![]() t=
t=![]() ×2
×2![]() ,
,
∴t=![]() .
.
如图4﹣2中,当MN⊥BC时,易知点F落在DH时,
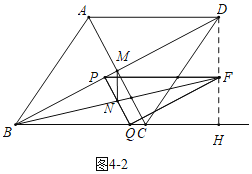
∵PF∥BH,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得t=![]() .
.
如图4﹣3中,当MN⊥AB时,易知∠PNM=∠ABD,
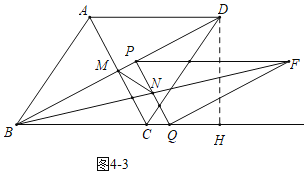
可得tan∠PNM=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得t=![]() ,
,
当点P与点D重合时,MN∥BC,此时t=2,
综上所述,满足条件的t的值为![]() 或
或![]() 或
或![]() 或2.
或2.