Question

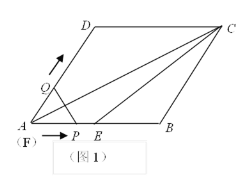
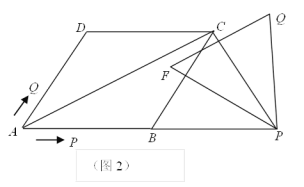
【题目】已知如图，正方形ABCD中，AD=4，点E在CD上，DE=3CE，F是AD上异于D的点，且∠EFB=∠FBC，则tan∠DFE=（ ）

A. 2 B. C. D.

Answer 1

【答案】D

【解析】

根据∠EFB=∠FBC，延长EF，BC相交于T，得到等腰△TBF，连接点T和MB的中点O，由△BAF∽△TOB，得到BF2=2AFBT，设CT=k，由DF∥CT，得=3，得出FD=3k，列出方程求出k，即可求出∠DFE的正切．

如图：延长EF交BC的延长线于T，设FB的中点为O，连TO，则OT⊥BF，

∵四边形ABCD是正方形，

∴AD=DC=BC=AB=4，∠D=ABC=∠A=90°，

∵∠ABF+∠OBT=90°，

∠OTB+∠OBT=90°，

∴∠ABF=∠OTB，则△BAF∽△TOB，

∴，

∵OB=BF，

∴BF2=2AFBT，

设CT=k，

∵CD=AD=4，DE=3EC，

∴DE=3，EC=1，

∵DF∥CT，

∴=3，

∴DF=3k，AF=4-3k，BT=4+k，

∴42+（4-3k）2=2×（4-3k）（4+k），

整理得到：15k2-8k=0，

∴k=或0（舍弃）．

∴tan∠DFE=．

故选D．