Question

【题目】已知，△ABC中，∠C=90°.

（1）若AC=4，BC=3，AE=，DE⊥AC．且DE=DB，求AD的长；

（2）请你用没有刻度的直尺和圆规，在线段AB上找一点F，使得点F到边AC的距离等于FB(注：不写作法，保留作图痕迹，对图中涉及到的点的用字母进行标注)

Answer 1

【答案】（1）．（2）作图见解析

【解析】

（1）根据DE∥BC，得出△ADE∽△ABC，进而得到，据此可得AD的长．

（2）作∠B的平分线BG，交AC于G，作BG的垂直平分线MN，交AB于F，则FG=FB，而FG∥BC，故FG⊥AC，即点F到边AC的距离等于FB．

（1）在Rt△ABC中，AC=4，BC=3，

∴AB=5，

∵DE⊥AC，∠C=90°，

∴DE∥BC，

∴△ADE∽△ABC，

∴，

即，

解得AD=，

故AD的长为．

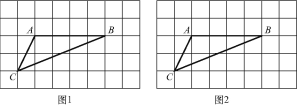
（2）如图2所示，作∠B的平分线BG，交AC于G，作BG的垂直平分线MN，交AB于F，则点F即为所求．