题目内容
3.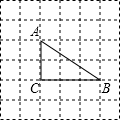 如图,在6×6的网格(小正方形的边长为1)中有一个△ABC,则AB边的长是$\sqrt{13}$,△ABC的周长是5+$\sqrt{13}$.
如图,在6×6的网格(小正方形的边长为1)中有一个△ABC,则AB边的长是$\sqrt{13}$,△ABC的周长是5+$\sqrt{13}$.
分析 AC、BC的长已知,根据勾股定理求出AB,再根据三角形周长的定义即可解答.
解答 解:根据题意,得:AC=2,BC=3.
根据勾股定理,得:AB=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$.
则三角形的周长是5+$\sqrt{13}$.
故答案为:$\sqrt{13}$,5+$\sqrt{13}$.
点评 本题考查了勾股定理的知识,解答本题的关键是在格点三角形中运用勾股定理求出三角形AB边的边长,难度一般.

练习册系列答案
相关题目
13.在平面直角坐标系中,将点A(-2,3)向上平移3个单位长度,再向右平移2个单位,那么平移后对应的点A′的坐标是( )
| A. | (-2,6) | B. | (-4,6) | C. | (0,0) | D. | (0,6) |
14.下列分式是最简分式的是( )
| A. | $\frac{2x}{{{x^2}+2}}$ | B. | $\frac{x-1}{{{x^2}-1}}$ | C. | $\frac{4}{2x}$ | D. | $\frac{1-x}{x-1}$ |
18. 将一副三角板按图中方式叠放,则∠α等于( )
将一副三角板按图中方式叠放,则∠α等于( )
 将一副三角板按图中方式叠放,则∠α等于( )
将一副三角板按图中方式叠放,则∠α等于( )| A. | 90° | B. | 75° | C. | 60° | D. | 45° |
15.下列各式中与a-b+c相等的是( )
| A. | a-(+b)-(+c) | B. | a-(+b)-(-c) | C. | a+(-b)+(-c) | D. | a+(-b)-(+c) |
12.下列各数是有理数的是( )
| A. | $3\sqrt{9}$ | B. | -π | C. | $\sqrt{8}$ | D. | $3\sqrt{27}$ |
13.计算(-4)2012×(-$\frac{1}{4}$)2011的结果是( )
| A. | 4 | B. | -4 | C. | 16 | D. | -16 |
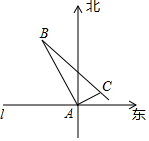 如图,在东西方向的海岸线l上有一观察站A,某时刻测得一艘沿匀速直线航行的轮船位于观察站A的北偏西30°且与观察站A相距40km的B处,经过1h20min,又测得该轮船位于观察站A的北偏东60°且与观察站A相距8$\sqrt{3}$km的C处,在求该轮船航行的速度(结果保留根号)
如图,在东西方向的海岸线l上有一观察站A,某时刻测得一艘沿匀速直线航行的轮船位于观察站A的北偏西30°且与观察站A相距40km的B处,经过1h20min,又测得该轮船位于观察站A的北偏东60°且与观察站A相距8$\sqrt{3}$km的C处,在求该轮船航行的速度(结果保留根号)