题目内容
 如图,△ABC是等腰三角形,D是底边BC上任意一点,DE⊥AB于点E,DF⊥AC于点F,若AB边上的高是6,求DE+DF的值.
如图,△ABC是等腰三角形,D是底边BC上任意一点,DE⊥AB于点E,DF⊥AC于点F,若AB边上的高是6,求DE+DF的值.考点:等腰三角形的性质
专题:
分析:连接AD,根据三角形的面积公式即可得到
AB•DE+
AC•DF=
AB×6,根据等腰三角形的性质进而求得DE+DF的值.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:连接AD,
解:连接AD,
∵AB边上的高是6,
∴S△ABC=
AB×6,
∵S△ABD=
AB•DE,S△ADC=
AC•DF,
∴
AB•DE+
AC•DF=
AB×6,
∵AB=AC,
∴
AB(DE+DF)=
AB×6,
∴DE+DF=6.
 解:连接AD,
解:连接AD,∵AB边上的高是6,
∴S△ABC=
| 1 |
| 2 |
∵S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=AC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴DE+DF=6.
点评:本题考查了等腰三角形的性质,三角形的面积,有利于培养同学们钻研和探索问题的精神.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
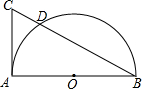 如图所示,AB为⊙O的直径,CA⊥AB,CD=1cm,DB=5cm,则AB=
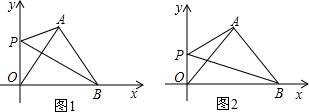
如图所示,AB为⊙O的直径,CA⊥AB,CD=1cm,DB=5cm,则AB= 如图,点A,B,C在一次函数y=-2x+5的图象上,它们的横坐标依次为-1,1,2,分别从这些点作x轴与y轴的垂线,则图中的阴影部分的面积之和是( )
如图,点A,B,C在一次函数y=-2x+5的图象上,它们的横坐标依次为-1,1,2,分别从这些点作x轴与y轴的垂线,则图中的阴影部分的面积之和是( )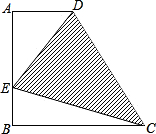 如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=x,AB=BC=2x,在线段AB上有一点E,∠DCE=45°,求tan∠DEC.
如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=x,AB=BC=2x,在线段AB上有一点E,∠DCE=45°,求tan∠DEC. 如图,AB是⊙O的直径,AC为弦,P为AC延长线上一点,且AC=PC,PB的延长线交⊙O于D,试说明:AC=DC.
如图,AB是⊙O的直径,AC为弦,P为AC延长线上一点,且AC=PC,PB的延长线交⊙O于D,试说明:AC=DC.