题目内容
20.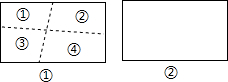 小明在折矩形纸活动中发现,如图①,1道折痕(折后展开,下同),将矩形分成2个部分,2道折痕最多将矩形分成4个部分,…,n道折痕最多将矩形分成F个部分,请解决下列问题:
小明在折矩形纸活动中发现,如图①,1道折痕(折后展开,下同),将矩形分成2个部分,2道折痕最多将矩形分成4个部分,…,n道折痕最多将矩形分成F个部分,请解决下列问题:(1)3道折痕最多可将矩形分成几个部分?并在图②中画出折痕;
(2)用n的代数式表示F;
(3)小明发现,当F在50与100之间时,n只有4个值,利用(2)的结论探究n的4个值.
分析 (1)画3道折痕(不要交于一点)即可得出结论.
(2)从特殊到一般可以归纳得出结论.
(3)列出不等式,解不等式组的正整数解.
解答 解:(13道折痕最多可将矩形分成7个部分,如图所示. (2)F=1+1+2+3+4+…+n=1+$\frac{n(n+1)}{2}$.
(2)F=1+1+2+3+4+…+n=1+$\frac{n(n+1)}{2}$.
(3)由题意:50≤1+$\frac{n(n+1)}{2}$≤100,
整理得:98≤n(n+1)≤198,
∵n是正整数,
∴n=10或11或12或13.
点评 本题考查翻折变换,解题的关键是从特殊到一般找到规律,学会用转化的思想解决问题.

练习册系列答案
相关题目
10.下列图形中,∠1与∠2互为补角的是( )
| A. |  | B. |  | C. |  | D. |  |
 有一块长10cm,宽5cm的铁皮,在它的四周各减去一个同样大的正方形,剩余的面积为30cm2,则切去的正方形的边长应为多少?
有一块长10cm,宽5cm的铁皮,在它的四周各减去一个同样大的正方形,剩余的面积为30cm2,则切去的正方形的边长应为多少?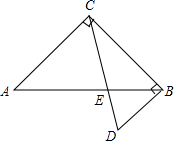 如图,将两块直角三角形的一条直角边重合叠放,已知AC=BC=$\sqrt{3}$+1,∠D=60°,则两条斜边的交点E到直角边BC的距离是1.
如图,将两块直角三角形的一条直角边重合叠放,已知AC=BC=$\sqrt{3}$+1,∠D=60°,则两条斜边的交点E到直角边BC的距离是1.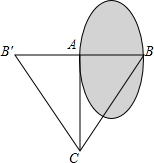 如图,测量水池的宽AB,可过点A作直线AC⊥AB,再由点C观测,在BA延长线上找一点B′,使∠ACB′=∠ACB,这时只要量出AB′的长,就知道AB的长,这个测量用到三角形全等判定方法是ASA.
如图,测量水池的宽AB,可过点A作直线AC⊥AB,再由点C观测,在BA延长线上找一点B′,使∠ACB′=∠ACB,这时只要量出AB′的长,就知道AB的长,这个测量用到三角形全等判定方法是ASA.