题目内容
4. 如图,已知△ABC≌△DEF,∠A=25°,∠B=105°,则∠F=50°.
如图,已知△ABC≌△DEF,∠A=25°,∠B=105°,则∠F=50°.
分析 根据三角形内角和定理求出∠ACB的度数,根据全等三角形的性质得到答案.
解答 解:∵∠A=25°,∠B=105°,
∴∠ACB=50°,
∵△ABC≌△DEF,
∴∠F=∠ACB=50°,
故答案为:50°.
点评 本题考查的是全等三角形的性质和三角形内角和定理,掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键.

练习册系列答案
相关题目
15.-5的绝对值的相反数的倒数是( )
| A. | $\frac{1}{5}$ | B. | -5 | C. | 5 | D. | -$\frac{1}{5}$ |
19.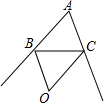 如图,在△ABC中,∠ABC和∠ACB的外角平分线交于点O,设∠A=m,则∠BOC=( )
如图,在△ABC中,∠ABC和∠ACB的外角平分线交于点O,设∠A=m,则∠BOC=( )
 如图,在△ABC中,∠ABC和∠ACB的外角平分线交于点O,设∠A=m,则∠BOC=( )
如图,在△ABC中,∠ABC和∠ACB的外角平分线交于点O,设∠A=m,则∠BOC=( )| A. | 90°-m | B. | 90°-$\frac{m}{2}$ | C. | 180°-2m | D. | 180°-$\frac{m}{2}$ |
14.已知实数a、b、c满足$\frac{b+c}{a}=\frac{a+c}{b}=\frac{a+b}{c}$=k (注:a+b+c≠0),则直线y=kx-k不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
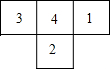 一个几何体由几个大小形状相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小立方块中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状.
一个几何体由几个大小形状相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小立方块中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状. 如图,已知△ABC中,∠ACB=90°.
如图,已知△ABC中,∠ACB=90°.