题目内容
12．
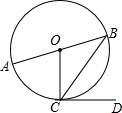如图，在⊙O中，AB为直径，BC为弦，CD为切线，连接OC．若∠BCD=50°，则∠AOC的度数为80°．
分析 根据切线的性质得出∠OCD=90°，进而得出∠OCB=40°，再利用圆心角等于圆周角的2倍解答即可．
解答 解：∵在⊙O中，AB为直径，BC为弦，CD为切线，
∴∠OCD=90°，
∵∠BCD=50°，
∴∠OCB=40°，
∴∠AOC=80°．
故答案为：80°．
点评 本题考查了切线的性质定理以及圆周角定理的运用，熟记和圆有关的各种性质定理是解题关键．
练习册系列答案
相关题目
如图，点A的坐标为（3，2），点B的坐标为（3，0）．作如下操作：
已知：直线AB、CD相交于O，∠1=40°，∠BOE与∠BOC互补，OM平分∠BOE，且∠CON：∠NOM=2：3，求∠COM和∠NOE的度数．
7．用配方法解方程x2-10x+9=0，配方后可得（ ）
| A． | （x-5）2=16 | B． | （x-5）2=1 | C． | （x-10）2=91 | D． | （x-10）2=109 |
17．下列各组中，不是同类项的是（ ）
| A． | 32与23 | B． | -3ab与ba | C． | 0.2a2b与$\frac{1}{5}{a^2}b$ | D． | a2b3与-a3b2 |
1．
在Rt△ACB中，∠C=90°，BC=5，AC=12，则sinA=（ ）
在Rt△ACB中，∠C=90°，BC=5，AC=12，则sinA=（ ）| A． | $\frac{5}{12}$ | B． | $\frac{12}{5}$ | C． | $\frac{5}{13}$ | D． | $\frac{12}{13}$ |
17．当a＞0＞b时，化简|a|-|b|-|a-b|+|b-a|的结果为（ ）
| A． | b-a | B． | 3a-b | C． | a+b | D． | 3b-a |