Question

13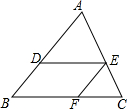．已知：如图，在△ABC中，DE∥BC，EF∥AB，$\frac{AD}{DB}$=$\frac{3}{2}$，BC=25，求：FC的长．

Answer 1

分析 先根据平行线分线段成比例定理，得出FC：BF=BD：AD，再根据AD：DB=3：2，得到BD：AD=2：3，进而得出FC：BC=2：5，即FC：25=2：5，据此可得FC=10．

解答 解：∵DE∥BC，
∴EC：AE=BD：AD，
∵EF∥AB，
∴EC：AE=FC：BF
∴FC：BF=BD：AD，
∵AD：DB=3：2，
∴BD：AD=2：3，
∴FC：BF=2：3，
∴FC：BC=2：5，
即FC：25=2：5
∴FC=10．

点评 本题主要考查了平行线分线段成比例定理的运用，解题时注意：平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例．