题目内容
8.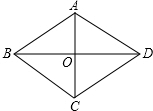 如图,在菱形ABCD中,AB=10,AC=12,则它的面积是96.
如图,在菱形ABCD中,AB=10,AC=12,则它的面积是96.
分析 首先根据勾股定理可求出BO的长,进而求出BD的长,再根据菱形的面积等于对角线乘积的一半列式计算即可得解.
解答 解:∵四边形ABCD是菱形,
∴AC⊥BD,
∵AC=12,
∴AO=6,
∵AB=10,
∴BO=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴BD=16,
∴菱形的面积S=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×16×12=96.
故答案为:96.
点评 本题考查了菱形的性质以及勾股定理的运用,熟练掌握菱形的面积等于对角线乘积的一半是解题的关键.

练习册系列答案
相关题目
18.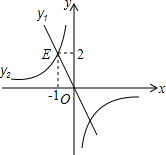 如图,正比例函数y1与反比例函数y2相交于点E(-1,2),若y1>y2>0,则x的取值范围是( )
如图,正比例函数y1与反比例函数y2相交于点E(-1,2),若y1>y2>0,则x的取值范围是( )
 如图,正比例函数y1与反比例函数y2相交于点E(-1,2),若y1>y2>0,则x的取值范围是( )
如图,正比例函数y1与反比例函数y2相交于点E(-1,2),若y1>y2>0,则x的取值范围是( )| A. | x<-1 | B. | -1<x<0 | C. | x>1 | D. | 0<x<1 |
20.下列式子:2a2b,3xy-2y2,$\frac{a+b}{2}$,4,-m,$\frac{x+yz}{2x}$,$\frac{ab-c}{π}$,其中是多项式的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
17.下列方程中,没有实数根的是( )
| A. | x2-4x+4=0 | B. | x2-2x+5=0 | C. | x2-2x=0 | D. | x2-2x-3=0 |
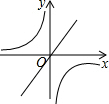
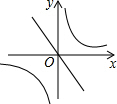
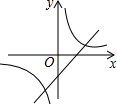
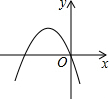 如果二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y=$\frac{b}{x}$在同一坐标系中的图象大致是( )
如果二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y=$\frac{b}{x}$在同一坐标系中的图象大致是( )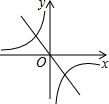
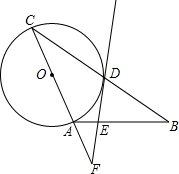 如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.