题目内容
3.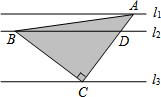 直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图放置,顶点A、B、C恰好分别落在三条直线上,则△ABC的面积为( )
直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为3.把一块含有45°角的直角三角板如图放置,顶点A、B、C恰好分别落在三条直线上,则△ABC的面积为( )| A. | $\frac{25}{4}$ | B. | $\frac{25}{2}$ | C. | 12 | D. | 25 |
分析 作BE⊥l3于E,作AF⊥l3于F,得出BE=3,AF=3+1=4,再证明△BEC≌△CFA,得出CE=AF,根据勾股定理求出BC,即可得出结果.
解答 解:作BE⊥l3于D,作AF⊥l3于F,如图所示: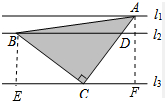 则∠BEC=∠CFA=90°,BE=3,AF=3+1=4,
则∠BEC=∠CFA=90°,BE=3,AF=3+1=4,
∴∠ECB+∠EBC=90°,
∵△ABC是等腰直角三角形,
∴∠ACB=90°,AC=BC,
∴∠ECB+∠FCA=90°,
∴∠EBC=∠FCA,
在△BEC和△CFA中,
$\left\{\begin{array}{l}{∠BEC=∠CFA}&{\;}\\{∠EBC=∠FCA}&{\;}\\{BC=AC}&{\;}\end{array}\right.$,
∴△BEC≌△CFA(AAS),
∴CE=AF=4,
∴BC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴AC=BC=5,
∴S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×5×5=$\frac{25}{2}$.
故选:B.
点评 本题考查了全等三角形的判定与性质、平行线之间的距离、勾股定理以及等腰直角三角形的性质;通过作辅助线证明三角形全等得出对应边相等是解决问题的关键.

练习册系列答案
相关题目
13.同一副三角板(两块)画角,不可能画出的角的度数是( )
| A. | 135° | B. | 75° | C. | 55° | D. | 15° |
14.在△ABC中,∠C=90°,AB=12,BC=5,则AC的长为( )
| A. | 12 | B. | 13 | C. | $\sqrt{119}$ | D. | 15 |
11.a=-0.32,b=-3-2,c=(-3)-2,d=(-$\frac{1}{3}$)0,则( )
| A. | a<b<d<c | B. | a<d<c<b | C. | b<a<c<d | D. | c<a<d<b |
18.下列说法中正确的个数是( )
①如果一个事件发生的可能性很小,那么他就不可能发生
②如果一个事件发生的概率很大,那么他就必然发生
③如果一个事件不可能发生,那么其发生的概率为0.
①如果一个事件发生的可能性很小,那么他就不可能发生
②如果一个事件发生的概率很大,那么他就必然发生
③如果一个事件不可能发生,那么其发生的概率为0.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 0个 |
8.下列不等式中,属于一元一次不等式的是( )
| A. | 4>1 | B. | 3x-2<4 | C. | $\frac{1}{x}$<2 | D. | 4x-3<2y-7 |
12.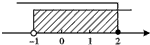 如图,下列哪个不等式组的解集在数轴上表示如图所示( )
如图,下列哪个不等式组的解集在数轴上表示如图所示( )
 如图,下列哪个不等式组的解集在数轴上表示如图所示( )
如图,下列哪个不等式组的解集在数轴上表示如图所示( )| A. | $\left\{\begin{array}{l}{x≤2}\\{x>-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x≥2}\\{x<-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x>2}\\{x≤-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x<2}\\{x≥-1}\end{array}\right.$ |
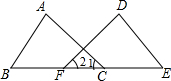 在数学实践课上,老师在黑板上画出如图的图形,(其中点B,F,C,E在同一条直线上).并写出四个条件:①AB=DE,②∠1=∠2.③BF=EC,④∠B=∠E,交流中老师让同学们从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题.
在数学实践课上,老师在黑板上画出如图的图形,(其中点B,F,C,E在同一条直线上).并写出四个条件:①AB=DE,②∠1=∠2.③BF=EC,④∠B=∠E,交流中老师让同学们从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题.