��Ŀ����
3����ͼ�����κ���y=$\frac{1}{2}$x2+bx-$\frac{3}{2}$��ͼ����x�ύ�ڵ�A��-3��0���͵�B����ABΪ����x���Ϸ���������ABCD����P��x����һ���㣬����DP������P��DP�Ĵ�����y�ύ�ڵ�E����1��b=1����D�����꣺��-3��4����
��2���߶�AO���Ƿ���ڵ�P����P����A��O�غϣ���ʹ��OE�ij�Ϊ1��
��3����x�Ḻ�������Ƿ���������ĵ�P��ʹ��PED�ǵ��������Σ������ڣ��������P�����꼰��ʱ��PED��������ABCD�ص����ֵ�������������ڣ���˵�����ɣ�

���� ��1�����õ��ڶ��κ���ͼ���ϣ����뼴�����b�������κ������ɽ���ʽ�����ܵó�B������꣬��AD=AB�����D�����ꣻ
��2��������ڣ���DP��AE���ҳ���EPO=��PDA�����õȽǵ�������ȣ��ɵó�һ������OP���ȵ�һԪ���η��̣��ɷ�����ɵ�֪�����������ĵ㣻
��3�����ýǺͱߵĹ�ϵ���ҵ�ȫ�ȣ����������������ƣ��������Ʊȼ������AM�������ADM�������������
��� �⣺��1���ߵ�A��-3��0���ڶ��κ���y=$\frac{1}{2}$x2+bx-$\frac{3}{2}$��ͼ���ϣ�
��0=$\frac{9}{2}$-3b-$\frac{3}{2}$�����b=1��
����κ�������ʽΪy=$\frac{1}{2}$x2+x-$\frac{3}{2}$=$\frac{1}{2}$��x+3����x-1����
���B��1��0����AB=1-��-3��=4��
���ı���ABCDΪ�����Σ�
��AD=AB=4��
���D��-3��4����
�ʴ�Ϊ��1����-3��4����
��2��ֱ��PE��y���ڵ�E����ͼ1��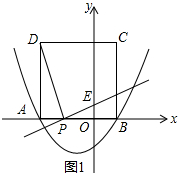
������ڵ�P��ʹ��OE�ij�Ϊ1����OP=a����AP=3-a��
��DP��AE����APD+��DPE+��EPO=180�㣬
���EPO=90��-��APD=��ADP��
tan��ADP=$\frac{AP}{AD}$=$\frac{3-a}{4}$��tan��EPO=$\frac{OE}{OP}$=$\frac{1}{a}$��
��$\frac{3-a}{4}$=$\frac{1}{a}$����a2-3a+4=0��
��=��-3��2-4��4=-7����
���߶�AO�ϲ����ڵ�P����P����A��O�غϣ���ʹ��OE�ij�Ϊ1��
��3��������������ĵ�P��DE��x���ڵ�M����ͼ2��
�ߡ�PED�ǵ��������Σ�
��DP=PE��
��DP��PE���ı���ABCDΪ������
���EPO+��APD=90�㣬��DAP=90�㣬��PAD+��APD=90�㣬
���EPO=��PDA����PEO=��DPA��
�ڡ�PEO�͡�DAP�У�
$\left\{\begin{array}{l}{��EPO=��PDA}\\{DP=PE}\\{��PEO=��DPA}\end{array}\right.$��
���PEO�ա�DAP��
��PO=DA=4��OE=AP=PO-AO=4-3=1��
���P������-4��0����
��DA��x�ᣬ
��DA��EO��
���ADM=��OEM����ֱ��ƽ�У��ڴ�����ȣ���
�֡ߡ�AMD=��OME���Զ��ǣ���
���DAM��EOM��
��$\frac{OM}{MA}$=$\frac{OE}{AD}$=$\frac{1}{4}$��
��OM+MA=OA=3��
��MA=$\frac{4}{1+4}$��3=$\frac{12}{5}$��
��PED��������ABCD�ص����֡�ADM���Ϊ$\frac{1}{2}$��AD��AM=$\frac{1}{2}$��4��$\frac{12}{5}$=$\frac{24}{5}$��
�𣺴��������ĵ�P����P������Ϊ��-4��1������ʱ��PED��������ABCD�ص����ֵ����Ϊ$\frac{24}{5}$��
���� ���⿼���˶��κ����Ľ���ʽ��ȫ�������ε��ж������������ε����Ʊȵ�֪ʶ������Ĺؼ���ע�����ν�ϣ���������ϵ��

| A�� | С��������4�� | B�� | С���ڵ���ǧ | ||
| C�� | ���ݴ�1¥��12¥ | D�� | һ����Ӹ߿��� |
 �ˣ�1����ͬѧΪ�˽�2015��ijС����ͥ�¾���ˮ�������������˸�С�����ּ�ͥ�������������ݽ�������������
�ˣ�1����ͬѧΪ�˽�2015��ijС����ͥ�¾���ˮ�������������˸�С�����ּ�ͥ�������������ݽ�������������| �¾���ˮ��x��t�� | Ƶ�������� | Ƶ�� |
| 0��x��5 | 6 | 0.12 |
| 5��x��10 | m | 0.24 |
| 10��x��15 | 16 | 0.32 |
| 15��x��20 | 10 | 0.20 |
| 20��x��25 | 4 | n |
| 60��x��70 | 2 | 0.04 |
��1����գ�m=12��n=0.08������Ƶ���ֲ�ֱ��ͼ����������
��2������С����1000����ͥ�����С���¾���ˮ������10t�ļ�ͥ��Լ�ж��ٻ���
| A�� | ����Խ��˵�����ݾ�Խ�ȶ� | |
| B�� | һԪ���η���x2-x+1=0����������ȵ�ʵ���� | |
| C�� | Բ�ڽ��ı��ζԽǻ��� | |
| D�� | ������һ�ߵĶԽǶ�Ӧ��ȵ�����������ȫ�� |
