题目内容
1.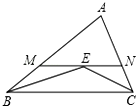 如图在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若AB+AC=7cm,则△AMN的周长为7cm.
如图在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若AB+AC=7cm,则△AMN的周长为7cm.
分析 根据角平分线的定义可得∠ABE=∠EBC,再根据两直线平行,内错角相等可得∠EBC=∠BEM,从而得到∠ABE=∠BEM,根据等角对等边的性质可得BM=EM,同理可得CN=EN,然后求出△AMN的周长=AB+AC,代入数据进行计算即可.
解答 解:∵EB平分∠ABC,
∴∠ABE=∠EEBC,
∵MN∥BC,
∴∠EBC=∠BEM,
∴∠ABE=∠BEM,
∴BM=EM,
同理可得CN=EN,
∴△AMN的周长=AM+ME+EN+AN=AM+BM+CN+AN=AB+AC,
∵AB+AC=7cm,
∴△AMN的周长=7cm.
故答案为:7.
点评 本题考查了等腰三角形的判定与性质,用到的知识点是等角对等边,两直线平行,内错角相等,熟记性质是解题的关键.

练习册系列答案
相关题目
9.下列计算正确的是( )
| A. | a2+a3=a5 | B. | a4÷a4=a | C. | a2•a3=a6 | D. | (-a2)3=-a6 |
16.下列由题意列出的不等关系中,错误的是( )
| A. | “a不是负数”表示为a>0 | |
| B. | “m与4的差是非负数”表示为m-4≥0 | |
| C. | “x不大于3”表示为x≤3 | |
| D. | “代数式x2+3大于3x-7”表示为x2+3>3x-7 |
6.等腰直角三角形的直角边为2,则斜边的长为( )
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 1 | D. | 2 |
13.△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列命题是假命题的是( )
| A. | 若∠C-∠B=∠A,则△ABC是直角三角形 | |
| B. | 若c2=b2-a2,则△ABC是直角三角形且∠C是直角 | |
| C. | 若(c+a)(c-a)=b2,则△ABC是直角三角形 | |
| D. | 若∠A:∠B:∠C=5:2:3,则△ABC是直角三角形且∠A为直角 |
 如图,AB∥CD,EF分别交AB、CD于点F、E,FG平分∠EFC,交AB于G;若∠1=80°,求∠FGE的度数.
如图,AB∥CD,EF分别交AB、CD于点F、E,FG平分∠EFC,交AB于G;若∠1=80°,求∠FGE的度数.