题目内容
14．
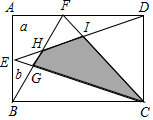如图，矩形ABCD中，E、F分别为AB、AD边上的点，四边形AEHF、△BEG、△FDI的面积分别为a、b、c，则阴影部分的面积为（ ）| A． | a+c | B． | a+b | C． | b+c | D． | a+b+c |
分析 由四边形ABCD是矩形，可得AB∥CD，AD∥BC，推出S△EDC=$\frac{1}{2}$S矩形ABCD，S△ABF+S△DFC=$\frac{1}{2}$S矩形ABCD，推出S△EDC=S△ABF+S△DFC，推出S△EGH+S阴+S△IDC=S△EBG+S△EGH+S四边形AEHF+S△FID+S△DIC，由此即可解决问题．
解答 解：∵四边形ABCD是矩形，
∴AB∥CD，AD∥BC，
∴S△EDC=$\frac{1}{2}$S矩形ABCD，S△ABF+S△DFC=$\frac{1}{2}$S矩形ABCD，
∴S△EDC=S△ABF+S△DFC，
∴S△EGH+S阴+S△IDC=S△EBG+S△EGH+S四边形AEHF+S△FID+S△DIC，
∴S阴=a+b+c，
故选D．
点评 本题考查矩形的性质，三角形的面积等知识，解题的关键是灵活运用所学知识解决问题，属于中考选择题中的压轴题．
练习册系列答案
名校课堂系列答案
相关题目
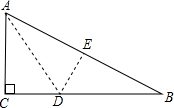如图，一块直角三角形的纸片，两直角边AC=6cm，BC=8cm．现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合．
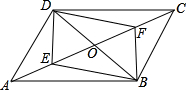如图，在平行四边形ABCD中，已知对角线AC、BD相交于点O，若E、F是AC上两动点，分别从A、C两点以相同的速度1cm/s向点O运动．
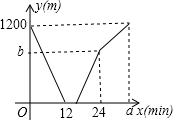甲、乙两人分别从A、B两地同时出发，相向而行，匀速前往B地、A地，两人相遇时停留了4min，又各自按原速前往目的地，甲、乙两人之间的距离y（m）与甲所用时间x（min）之间的函数关系如图所示．有下列说法：